题目内容
已知A,B,C是三角形△ABC三内角,向量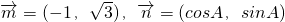 ,且
,且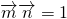
(Ⅰ)求角A;
(Ⅱ)若a=2,△ABC的面积等于 ,求b,c.
,求b,c.
解:(Ⅰ)∵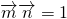 ,∴
,∴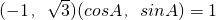 ,
,
所以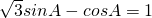
进而可得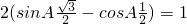 ,
,
∵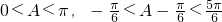 ,
,
∴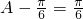 ,∴
,∴
(Ⅱ)由余弦定理得,b2+c2-bc=4
又因为△ABC的面积等于 ,所以
,所以 ,得bc=4.
,得bc=4.
联立方程组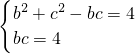 ,解得b=2,c=2.
,解得b=2,c=2.
分析:(Ⅰ)由数量积和三角函数的性质可得 ,由A的范围可得A的值;(Ⅱ)由余弦定理和面积可得b、c的方程组,解之即可.
,由A的范围可得A的值;(Ⅱ)由余弦定理和面积可得b、c的方程组,解之即可.
点评:本题考查平面向量的数量积,涉及三角函数的化简和余弦定理,属中档题.
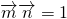 ,∴
,∴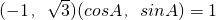 ,
,所以
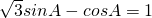
进而可得
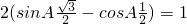 ,
,
∵
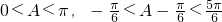 ,
,∴
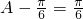 ,∴
,∴
(Ⅱ)由余弦定理得,b2+c2-bc=4
又因为△ABC的面积等于
 ,所以
,所以 ,得bc=4.
,得bc=4.联立方程组
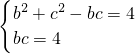 ,解得b=2,c=2.
,解得b=2,c=2.分析:(Ⅰ)由数量积和三角函数的性质可得
 ,由A的范围可得A的值;(Ⅱ)由余弦定理和面积可得b、c的方程组,解之即可.
,由A的范围可得A的值;(Ⅱ)由余弦定理和面积可得b、c的方程组,解之即可.点评:本题考查平面向量的数量积,涉及三角函数的化简和余弦定理,属中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 中的最大数为
中的最大数为 ,最小数为
,最小数为 已知
已知 的三边边长为a,b,c(
的三边边长为a,b,c( ),定义它的倾斜度为
),定义它的倾斜度为
 是“
是“ ,则△ABC为( )
,则△ABC为( ) ,则△ABC为( )
,则△ABC为( )