题目内容
已知函数f(x)=2acos2x+bsinxcosx,且f(0)=2,f(
)=
+
.(1)求a，b的值；
(2)求f(x)的最大值及取得最大值时x的集合；
(3)写出函数f(x)在［0，π］上的单调递减区间.
解:(1)由题意得方程组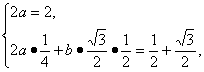解得
(2)由(1)有f(x)=2cos2x+2sinxcosx=1+cos2x+sin2x
=1+sin(2x+
),
∴当2x+
=2kπ+
(k∈Z),
即x=kπ+
(k∈Z)时，f(x)取得最大值1+
,
∴f(x)的最大值为1+
.
取到最大值时x的集合是{x|x=kπ+
,k∈Z}.
(3)∵x∈［0,π］,
∴2x+
∈［
,
］.要使函数f(x)递减，
则应2x+
∈［
,
］,可得x∈［
,
］,
∴函数f(x)在［0,π］上的递减区间为［
,
］.
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目