题目内容
求（a-2b-3c）10的展开式中含a3b4c3项的系数．
分析：利用分布乘法原理含a3b4c3项是三个括号出a，四个括号出-2b，三个括号出-3c形成．
解答：解：（a-2b-3c）10=（a-2b-3c）（a-2b-3c）（a-2b-3c），
从10个括号中任取3个括号，从中取a；再从剩余7个括号中任取4个括号，
从中取-2b；最后从剩余的3个括号中取-3c，
得含a3b4c3的项为C103a3C74•（-2b）4C33（-3c）3=C103C74C3324（-3）3a3b4c3．
所以含a3b4c3项的系数为-C103C74×16×27．
从10个括号中任取3个括号，从中取a；再从剩余7个括号中任取4个括号，
从中取-2b；最后从剩余的3个括号中取-3c，
得含a3b4c3的项为C103a3C74•（-2b）4C33（-3c）3=C103C74C3324（-3）3a3b4c3．
所以含a3b4c3项的系数为-C103C74×16×27．
点评：解决一些较复杂的式子的展开式的特定项问题分步乘法计数原理是最基本的方法．
练习册系列答案
相关题目
+
+
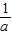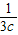=m，求 Z=a+2b+3c的最小值．