题目内容
(本小题满分12分)
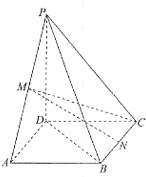
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M、N分别为PA、BC的中点, PD⊥平面ABCD,且PD=AD=![]() ,CD=1.
,CD=1.
(Ⅰ)证明:MN∥平面PCD;
(Ⅱ)证明:MC⊥BD;
(Ⅲ)求二面角A—PB—D的余弦值.
解:(Ⅰ)证明:取AD中点E,连接ME,NE,
由已知M,N分别是PA,BC的中点,
∴ME∥PD,NE∥CD
又ME,NE![]() 平面MNE,ME
平面MNE,ME![]() NE=E,
NE=E,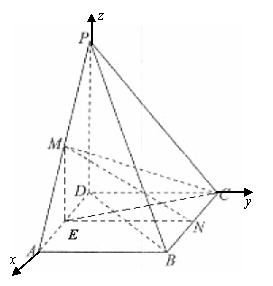
所以,平面MNE∥平面PCD,又MN![]() 平面MNE
平面MNE
所以,MN∥平面PCD ……………4分
(Ⅱ)因为PD⊥平面ABCD,所以PD⊥DA,PD⊥DC,
在矩形ABCD中,AD⊥DC,
如图,以D为坐标原点,射线DA,DC,DP分别为
![]() 轴、
轴、![]() 轴、
轴、![]() 轴正半轴建立空间直角坐标系.
轴正半轴建立空间直角坐标系.
则D(0,0,0),A(![]() ,0,0),
,0,0),
B(![]() ,1,0),
,1,0),![]() (0,1,0), P(0,0,
(0,1,0), P(0,0,![]() )
)
所以![]() (
(![]() ,0,
,0,![]() ),
),![]() ,
,![]()
∵![]() ·
·![]() =0,所以MC⊥BD ……………8分
=0,所以MC⊥BD ……………8分
(Ⅲ)因为ME∥PD,所以ME⊥平面ABCD,ME⊥BD,又BD⊥MC,
所以BD⊥平面MCE, 所以CE⊥BD,又CE⊥PD,所以CE⊥平面PBD,
由已知![]() ,所以平面PBD的法向量
,所以平面PBD的法向量![]()
M为等腰直角三角形PAD斜边中点,所以DM⊥PA,
又CD⊥平面PAD,AB∥CD,所以AB⊥平面PAD,AB⊥DM,所以DM⊥平面PAB,
所以平面PAB的法向量![]() (-
(-![]() ,0,
,0,![]() ),设二面角A—PB—D的平面角为θ,
),设二面角A—PB—D的平面角为θ,
则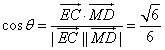 . 所以,二面角A—PB—D的余弦值为
. 所以,二面角A—PB—D的余弦值为![]() . ……………12分
. ……………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目