题目内容
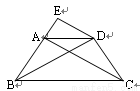
如图,等腰梯形ABCD中,AB∥CD且AB=2,AD=1,DC=2x(x∈(0,1)).以A,B为焦点,且过点D的双曲线的离心率为e1;以C,D为焦点,且过点A的椭圆的离心率为e2,则e1+e2的取值范围为 ( )
A.[2,+∞)
B.(
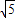 ,+∞)
,+∞)C.[
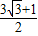 ,+∞)
,+∞)D.(
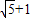 ,+∞)
,+∞)
【答案】分析:连接BD、AC,设∠DAB=θ,θ∈(0,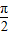 ),根据余弦定理表示出BD,进而根据双曲线的性质可得到a的值,再由AB=2c,e=
),根据余弦定理表示出BD,进而根据双曲线的性质可得到a的值,再由AB=2c,e=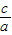 可表示出e1,同样表示出椭圆中的c'和a'表示出e2的关系式,最后令e1、e2相乘即可得到e1e2的值,最后利用基本不等式求出e1+e2的取值范围即可.
可表示出e1,同样表示出椭圆中的c'和a'表示出e2的关系式,最后令e1、e2相乘即可得到e1e2的值,最后利用基本不等式求出e1+e2的取值范围即可.
解答: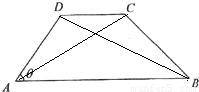 解:连接BD,AC,设∠DAB=θ,θ∈(0,
解:连接BD,AC,设∠DAB=θ,θ∈(0,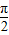 ),
),
则BD=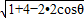 =
=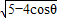 ,
,
∴双曲线中a=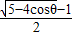 ,e1=
,e1=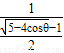 .
.
∵AC=BD,
∴椭圆中CD=2t(1-cosθ)=2c′,
∴c'=t(1-cosθ),
AC+AD=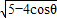 +1,
+1,
∴a'= (
( 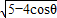 +1)
+1)
e2=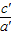 =
=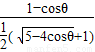 ,
,
∴e1e2=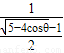 ×
×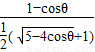 =1,
=1,
∴e1+e2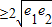 =2,即则e1+e2的取值范围为[2,+∞).
=2,即则e1+e2的取值范围为[2,+∞).
故选A.
点评:本小题主要考查椭圆的简单性质、双曲线的简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.
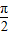 ),根据余弦定理表示出BD,进而根据双曲线的性质可得到a的值,再由AB=2c,e=
),根据余弦定理表示出BD,进而根据双曲线的性质可得到a的值,再由AB=2c,e=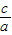 可表示出e1,同样表示出椭圆中的c'和a'表示出e2的关系式,最后令e1、e2相乘即可得到e1e2的值,最后利用基本不等式求出e1+e2的取值范围即可.
可表示出e1,同样表示出椭圆中的c'和a'表示出e2的关系式,最后令e1、e2相乘即可得到e1e2的值,最后利用基本不等式求出e1+e2的取值范围即可.解答:
 解:连接BD,AC,设∠DAB=θ,θ∈(0,
解:连接BD,AC,设∠DAB=θ,θ∈(0,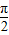 ),
),则BD=
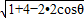 =
=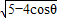 ,
,∴双曲线中a=
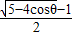 ,e1=
,e1=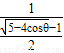 .
.∵AC=BD,
∴椭圆中CD=2t(1-cosθ)=2c′,
∴c'=t(1-cosθ),
AC+AD=
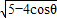 +1,
+1,∴a'=
 (
( 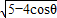 +1)
+1)e2=
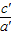 =
=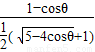 ,
,∴e1e2=
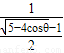 ×
×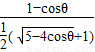 =1,
=1,∴e1+e2
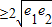 =2,即则e1+e2的取值范围为[2,+∞).
=2,即则e1+e2的取值范围为[2,+∞).故选A.
点评:本小题主要考查椭圆的简单性质、双曲线的简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目
 (2013•惠州一模)如图,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2
(2013•惠州一模)如图,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2