题目内容
已知数列bn前n项和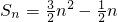 .数列an满足
.数列an满足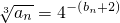 (n∈N*),数列cn满足cn=anbn.
(n∈N*),数列cn满足cn=anbn.
(1)求数列an和数列bn的通项公式;
(2)求数列cn的前n项和Tn;
(3)若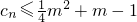 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.
解:(1)由已知和得,当n≥2时, (2分)
(2分)
又b1=1=3×1-2,符合上式.故数列bn的通项公式bn=3n-2.(3分)
又∵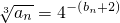 ,∴
,∴ ,
,
故数列an的通项公式为 ,(5分)
,(5分)
(2) ,
, ,①
,① ,②
,②
①-②得 =
= =
= ,
,
∴ . (10分)
. (10分)
(3)∵ ,
,
∴ =
= ,
,
当n=1时,cn+1=cn;当n≥2时,cn+1≤cn,∴ .
.
若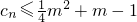 对一切正整数n恒成立,则
对一切正整数n恒成立,则 即可,
即可,
∴m2+4m-5≥0,即m≤-5或m≥1. (14分).
分析:(1)利用bn=Sn-Sn-1求出数列bn的通项公式,然后利用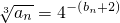 求出数列an通项公式;
求出数列an通项公式;
(2)利用cn=anbn.求出数列cn的通项公式,写出前n项和Tn的表达式,利用错位相减法,求出前n项和Tn.
(3)求出数列cn的最大值,利用 ,求出m的取值范围.
,求出m的取值范围.
点评:本题考查数列的通项公式的求法,数列求和等基础知识,考查计算能力、推理论证能力、综合发现问题解决问题的能力.
 (2分)
(2分)又b1=1=3×1-2,符合上式.故数列bn的通项公式bn=3n-2.(3分)
又∵
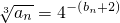 ,∴
,∴ ,
,故数列an的通项公式为
 ,(5分)
,(5分)(2)
 ,
, ,①
,① ,②
,②①-②得
 =
= =
= ,
,∴
 . (10分)
. (10分)(3)∵
 ,
,∴
 =
= ,
,当n=1时,cn+1=cn;当n≥2时,cn+1≤cn,∴
 .
.若
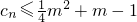 对一切正整数n恒成立,则
对一切正整数n恒成立,则 即可,
即可,∴m2+4m-5≥0,即m≤-5或m≥1. (14分).
分析:(1)利用bn=Sn-Sn-1求出数列bn的通项公式,然后利用
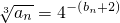 求出数列an通项公式;
求出数列an通项公式;(2)利用cn=anbn.求出数列cn的通项公式,写出前n项和Tn的表达式,利用错位相减法,求出前n项和Tn.
(3)求出数列cn的最大值,利用
 ,求出m的取值范围.
,求出m的取值范围.点评:本题考查数列的通项公式的求法,数列求和等基础知识,考查计算能力、推理论证能力、综合发现问题解决问题的能力.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
 .数列an满足
.数列an满足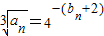 (n∈N*),数列cn满足cn=anbn.
(n∈N*),数列cn满足cn=anbn.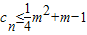 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.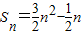 .数列an满足
.数列an满足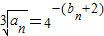 (n∈N*),数列cn满足cn=anbn.
(n∈N*),数列cn满足cn=anbn.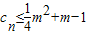 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.