题目内容
课本是这样定义增函数的（如图文字）
证明：函数f(x)=1-
，在区间（-∞，0）上是增函数．
证明：函数f(x)=1-
| 1 | x |
分析：设x1＜x2＜0，根据增函数的定义，只需通过作差证明f（x1）＜f（x2）即可．
解答：证明：设x1＜x2＜0，
则f（x1）-f（x2）=（1-
）-（1-
）=
，
因为x1＜x2＜0，所以x1-x2＜0，x1x2＞0，
所以f（x1）-f（x2）＜0，即f（x1）＜f（x2）．
故函数f(x)=1-
，在区间（-∞，0）上是增函数．
则f（x1）-f（x2）=（1-
| 1 |
| x1 |
| 1 |
| x2 |
| x1-x2 |
| x1x2 |
因为x1＜x2＜0，所以x1-x2＜0，x1x2＞0，
所以f（x1）-f（x2）＜0，即f（x1）＜f（x2）．
故函数f(x)=1-
| 1 |
| x |
点评：本题考查函数单调性的证明，需要根据定义严格证明，如无方法要求运用导数证明也可，属基础题．
练习册系列答案
相关题目
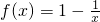，在区间（-∞，0）上是增函数．
，在区间（-∞，0）上是增函数．