题目内容
已知函数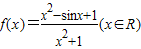 存在最大值M和最小值N,则M+N的值为 .
存在最大值M和最小值N,则M+N的值为 .
【答案】分析:令g(x)=- ,则f(x)=1+g(x),f(x)的最大值M等于g(x)的最大值m加上1,f(x)的最小值N 等于g(x)的最小值n加上1,故M+N=m+1+n+1.再由g(x)是奇函数,
,则f(x)=1+g(x),f(x)的最大值M等于g(x)的最大值m加上1,f(x)的最小值N 等于g(x)的最小值n加上1,故M+N=m+1+n+1.再由g(x)是奇函数,
故m+n=0,由此求得M+N的值.
解答:解:∵函数 =1-
=1- ,令g(x)=-
,令g(x)=-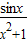 ,则有f(x)=1+g(x),且g(x)是奇函数.
,则有f(x)=1+g(x),且g(x)是奇函数.
故f(x)的最大值M等于g(x)的最大值m加上1,即 M=m+1. f(x)的最小值N等于g(x)的最小值n加上1,即N=n+1.
再由于g(x)是奇函数,由奇函数的性质可得 m+n=0,故M+N=m+1+n+1=2,
故答案为2.
点评:本题主要考查函数的奇偶性的应用,属于基础题.
 ,则f(x)=1+g(x),f(x)的最大值M等于g(x)的最大值m加上1,f(x)的最小值N 等于g(x)的最小值n加上1,故M+N=m+1+n+1.再由g(x)是奇函数,
,则f(x)=1+g(x),f(x)的最大值M等于g(x)的最大值m加上1,f(x)的最小值N 等于g(x)的最小值n加上1,故M+N=m+1+n+1.再由g(x)是奇函数,故m+n=0,由此求得M+N的值.
解答:解:∵函数
 =1-
=1- ,令g(x)=-
,令g(x)=-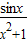 ,则有f(x)=1+g(x),且g(x)是奇函数.
,则有f(x)=1+g(x),且g(x)是奇函数.故f(x)的最大值M等于g(x)的最大值m加上1,即 M=m+1. f(x)的最小值N等于g(x)的最小值n加上1,即N=n+1.
再由于g(x)是奇函数,由奇函数的性质可得 m+n=0,故M+N=m+1+n+1=2,
故答案为2.
点评:本题主要考查函数的奇偶性的应用,属于基础题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 存在最大值M和最小值N, 则M+N的值为
存在最大值M和最小值N, 则M+N的值为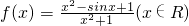 存在最大值M和最小值N,则M+N的值为________.
存在最大值M和最小值N,则M+N的值为________. 存在最大值M和最小值N,则M+N的值为 .
存在最大值M和最小值N,则M+N的值为 . 存在最大值M和最小值N,则M+N的值为 .
存在最大值M和最小值N,则M+N的值为 .