Question

（本小题满分12分）

    某单位有三辆汽车参加某种事故保险，年初向保险公司缴纳每辆900元的保险金，对在一年内发生此种事故的每辆汽车，单位可获9000元的赔偿（假设每辆车每年最多只赔偿一次），设这三辆车在一年内发生此种事故的概率分别为、、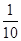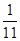，且各车是否发生事故相互独立，求一年内该单位在此保险中：

   （Ⅰ）获赔的概率；

   （Ⅱ）获赔金额ξ的分布列与期望．

 

Answer 1

【答案】

 

(1)

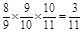
(2) ξ的分布列为

ξ	0	9000	18000	27000
P

由ξ的分布列得

Eξ=(元)

【解析】解：设Ak表示第k辆车在一年内发生此种事故，k=1，2，3.由题意知A1、A2、A3相互独立，

且P(A1)=，P(A2)=，P(A3)=. ………………………………………2分

(Ⅰ)该单位一年内获赔的概率为

1-P()=1-P()P()P()=1-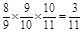. ……………………4分

(Ⅱ)ξ的所有可能值为0，9000，18000，27000.                         

P(ξ=0)=P()=P()P()P()=，             

P(ξ=9000)=P(A1)+P(A2)+P(A3)

=P(A1)P()P()+P()P(A2)P()+P()P()P(A3)

=，………………………6分

P(ξ=18000)=P(A1A2)+P(A1A3)+P(A2A3)

=P(A1)P(A2)P()+P(A1)P()P(A3)+P()P(A2)P(A3)

=，                           

P(ξ=27000)=P(A1A2A3)=P(A1)P(A2)P(A3)=. …………………8分

综上知，ξ的分布列为

Tesoon.com  天星版权   ξ	0	9000	18000	27000
P

由ξ的分布列得

Eξ=(元)   …………12分