题目内容
16.把-块边长为10cm正方形铁片按如图所示的阴影部分裁下,用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足是底面中心的四棱锥)形容器,(1)试建立容器的容积V与所截等腰三角形的底边边长为x的函数关系式,并求出函数的定义域.
(2)试求容积V的最大值;
(3)当x=$\frac{10\sqrt{3}}{3}$时,M是BC的中点,P是EB上一点,求AP+PM最小值.

分析 (1)由图可知:EO⊥平面ABCD,EF=5,OF=$\frac{1}{2}x$,EO=$\sqrt{E{F}^{2}-O{F}^{2}}$.利用V=$\frac{1}{3}•EO•{S}_{正方形ABCD}$剪开得出.
(2)设$\sqrt{100-{x}^{2}}$=t∈(0,10),则x2=100-t2.可得V=$\frac{1}{6}$t(100-t2)=$\frac{1}{6}(100t-{t}^{3})$=f(t),利用导数研究其单调性极值与最值即可得出.
(3)把△EAB,△EBC,剪开在同一个平面内,连接AM交EB于点P.当x=$\frac{10\sqrt{3}}{3}$时,tan∠EBA=$\sqrt{3}$,可得∠EBA=60°.∠ABM=120°.在△ABM中,利用余弦定理即可得出.
解答  解:(1)由图可知:EO⊥平面ABCD,
解:(1)由图可知:EO⊥平面ABCD,
EF=5,OF=$\frac{1}{2}x$,EO=$\sqrt{E{F}^{2}-O{F}^{2}}$=$\sqrt{{5}^{2}-\frac{{x}^{2}}{4}}$=$\frac{\sqrt{100-{x}^{2}}}{2}$.
∴V=$\frac{1}{3}•EO•{S}_{正方形ABCD}$=$\frac{1}{3}×\frac{\sqrt{100-{x}^{2}}}{2}$×x2(0<x<10).
(2)设$\sqrt{100-{x}^{2}}$=t∈(0,10),则x2=100-t2.
∴V=$\frac{1}{6}$t(100-t2)=$\frac{1}{6}(100t-{t}^{3})$=f(t),
则f′(t)=$\frac{1}{6}(100-3{t}^{2})$=$\frac{-(t+\sqrt{\frac{100}{3}})(t-\sqrt{\frac{100}{3}})}{2}$,
当$t∈(0,\sqrt{\frac{100}{3}})$时,f′(t)>0,函数f(t)单调递增;当$t∈(\sqrt{\frac{100}{3}},10)$时,f′(t)<0,函数f(t)单调递减.
∴当t=$\sqrt{\frac{100}{3}}$即x=$\frac{10\sqrt{6}}{3}$时,f(t)取得最大值$\frac{1000\sqrt{3}}{27}$cm3.
(3)把△EAB,△EBC,剪开在同一个平面内,连接AM交EB于点P.当x=$\frac{10\sqrt{3}}{3}$时,tan∠EBA=$\frac{5}{\frac{1}{2}×\frac{10\sqrt{3}}{3}}$=$\sqrt{3}$,∴∠EBA=60°.
∴∠ABM=120°.
在△ABM中,由余弦定理可得:AM2=$(\frac{10\sqrt{3}}{3})^{2}$+$(\frac{5\sqrt{3}}{3})^{2}$-$2×\frac{10\sqrt{3}}{3}×\frac{5\sqrt{3}}{3}×cos12{0}^{°}$=$\frac{175}{3}$.
∴AM=$\frac{5\sqrt{21}}{3}$.
∴AP+PM最小值为AM=$\frac{5\sqrt{21}}{3}$.
点评 本题考查了空间位置关系、体积计算、勾股定理、余弦定理,考查了推理能力与计算能力,属于中档题.

| A. | (x+1)2+(y-1)2=1 | B. | (x-1)2+(y+1)2=1 | ||
| C. | (x+1)2+(y+1)2=1 | D. | (x+1)2+(y-1)2=1或(x-1)2+(y+1)2=1 |
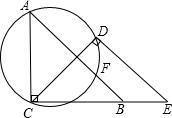 已知,如图∠A=45°,∠ACE=∠CDE=90°,点B在CE上,CB=CD,过A、C、D三点的圆交AB于点F,求证:点F是△CDE的内心.
已知,如图∠A=45°,∠ACE=∠CDE=90°,点B在CE上,CB=CD,过A、C、D三点的圆交AB于点F,求证:点F是△CDE的内心.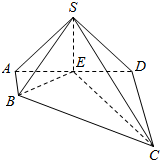 如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=$\sqrt{3}$,SE⊥AD.
如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=$\sqrt{3}$,SE⊥AD.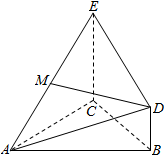 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE且CE=CA=2BD,M是EA的中点.
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE且CE=CA=2BD,M是EA的中点.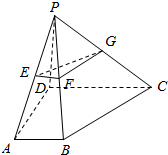 如图,四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}AD$=1.
如图,四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}AD$=1.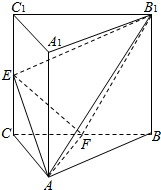 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,E,F分别是CC1,BC的中点.