题目内容
已知函数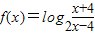
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性;
(3)讨论f(x)的单调性,并证明.
【答案】分析:(1)由题,可令 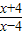 >0,解出函数的定义域.
>0,解出函数的定义域.
(2)由f(-x)=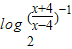 =-f(x),依据奇函数定义得出函数的奇偶性.
=-f(x),依据奇函数定义得出函数的奇偶性.
(3)再由复合函数单调性的判断方法判断出单调性即可.
解答:解:(1)由题意,令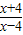 >0,解得4<x或x<-4,故函数的定义域为(-∞,-4)∪(4,+∞)
>0,解得4<x或x<-4,故函数的定义域为(-∞,-4)∪(4,+∞)
(2)由于f(-x)=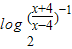 =-f(x),∴函数是奇函数.
=-f(x),∴函数是奇函数.
(3)当x∈(-∞,-4)∪(4,+∞)时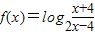
可知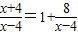 .
.
因为y=x-4是增函数
y=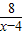 是减函数
是减函数
y=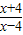 是减函数
是减函数
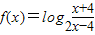 是减函数
是减函数
综上,函数的定义域为(-∞,-4)∪(4,+∞),此函数是一个奇函数,也是减函数.
点评:本题考点是对数函数图象与性质的应用,考察了对数函数定义域的求法,对数的运算性质,函数奇偶性的判断,复合函数单调性的判断规则,解题的关键是熟练掌握对数的性质、复合函数单调性的判断规则,本题考察了推理判断的能力.
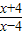 >0,解出函数的定义域.
>0,解出函数的定义域.(2)由f(-x)=
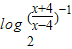 =-f(x),依据奇函数定义得出函数的奇偶性.
=-f(x),依据奇函数定义得出函数的奇偶性.(3)再由复合函数单调性的判断方法判断出单调性即可.
解答:解:(1)由题意,令
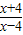 >0,解得4<x或x<-4,故函数的定义域为(-∞,-4)∪(4,+∞)
>0,解得4<x或x<-4,故函数的定义域为(-∞,-4)∪(4,+∞)(2)由于f(-x)=
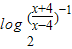 =-f(x),∴函数是奇函数.
=-f(x),∴函数是奇函数.(3)当x∈(-∞,-4)∪(4,+∞)时
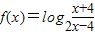
可知
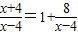 .
.因为y=x-4是增函数
y=
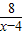 是减函数
是减函数y=
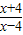 是减函数
是减函数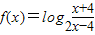 是减函数
是减函数综上,函数的定义域为(-∞,-4)∪(4,+∞),此函数是一个奇函数,也是减函数.
点评:本题考点是对数函数图象与性质的应用,考察了对数函数定义域的求法,对数的运算性质,函数奇偶性的判断,复合函数单调性的判断规则,解题的关键是熟练掌握对数的性质、复合函数单调性的判断规则,本题考察了推理判断的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.

