题目内容
(1)研究函数f(x)=lnx-x的单调区间与极值.
(2)试探究f(x)=lnx-ax(a∈R)单调性.
解:(1)f′(x)= -1=
-1=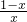 ,
,
令f′(x)<0得x>1
令f′(x)>0得0<x<1
所以函数f(x)=lnx-x的单调减区间是(1,+∞),单调递增区间是(0,1).
∴f(x)在x=1处取得极大值-1,无极大值.
(2)f′(x)= -a…(2分)
-a…(2分)
(Ⅰ)∵x>0,所以当a≤0时,f′(x)= -a>0,f(x)在(0,+∞)是增函数…(4分)
-a>0,f(x)在(0,+∞)是增函数…(4分)
当a>0时,f(x)在(0, )上f′(x)=
)上f′(x)= -a>0,f(x)在(
-a>0,f(x)在( ,+∞)上f′(x)=
,+∞)上f′(x)= -a<0,
-a<0,
故f(x)在(0, )上是增函数,f(x)在(
)上是增函数,f(x)在( ,+∞)上是减函数.
,+∞)上是减函数.
分析:(1)先求出函数的定义域,求出函数f(x)的导函数,在定义域下令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间.
(2)首先求出函数的导数,然后根据导数与单调区间的关系确定函数的单调区间.
点评:本题主要考查导数与函数单调性的关系,会熟练运用导数解决函数的极值与最值问题.求函数的单调区间,应该先求出函数的导函数,令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间.
 -1=
-1=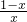 ,
,令f′(x)<0得x>1
令f′(x)>0得0<x<1
所以函数f(x)=lnx-x的单调减区间是(1,+∞),单调递增区间是(0,1).
∴f(x)在x=1处取得极大值-1,无极大值.
(2)f′(x)=
 -a…(2分)
-a…(2分)(Ⅰ)∵x>0,所以当a≤0时,f′(x)=
 -a>0,f(x)在(0,+∞)是增函数…(4分)
-a>0,f(x)在(0,+∞)是增函数…(4分)当a>0时,f(x)在(0,
 )上f′(x)=
)上f′(x)= -a>0,f(x)在(
-a>0,f(x)在( ,+∞)上f′(x)=
,+∞)上f′(x)= -a<0,
-a<0,故f(x)在(0,
 )上是增函数,f(x)在(
)上是增函数,f(x)在( ,+∞)上是减函数.
,+∞)上是减函数.分析:(1)先求出函数的定义域,求出函数f(x)的导函数,在定义域下令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间.
(2)首先求出函数的导数,然后根据导数与单调区间的关系确定函数的单调区间.
点评:本题主要考查导数与函数单调性的关系,会熟练运用导数解决函数的极值与最值问题.求函数的单调区间,应该先求出函数的导函数,令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目