题目内容
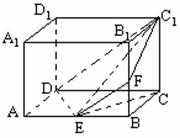
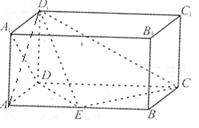
如图,长方体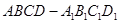 中,
中,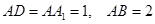 ,点
,点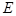 是
是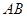 的中点.
的中点.
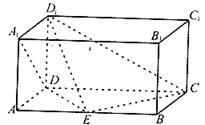
(1)求三棱锥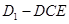 的体积;
的体积;
(2)证明: ;
;
(3)求二面角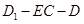 的正切值.
的正切值.
【答案】
(1)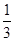 ;(2)证明过程详见解析;(3)
;(2)证明过程详见解析;(3)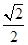 .
.
【解析】
试题分析:本题主要考查空间两条直线的位置关系、二面角、锥体体积等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算能力、推理论证能力.第一问,求锥体体积,关键是找到锥体的高和底面面积;第二问,先利用直线与平面的判定定理证出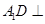 面
面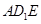 ,所以
,所以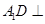 面内的线段
面内的线段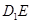 ;第三问,先利用直线与平面的判定定理证出
;第三问,先利用直线与平面的判定定理证出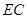
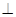 面
面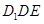 ,所以
,所以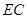
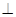 面内的线段
面内的线段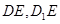 ,所以就找到了二面角的平面角,在直角三角形中求正切.
,所以就找到了二面角的平面角,在直角三角形中求正切.
试题解析:(1)由长方体性质可得,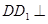 面
面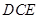 ,所以
,所以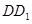 是三棱锥
是三棱锥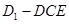 的高,
的高,
又点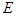 是
是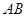 的中点,
的中点,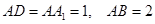 , 所以,
, 所以,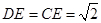 ,
,
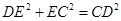
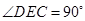 2分
2分
三棱锥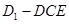 的体积
的体积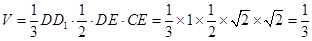 4分
4分
(2)
连结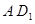 , 因为
, 因为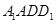 是正方形,所以
是正方形,所以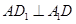
又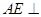 面
面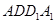
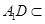 面
面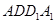 ,
,
所以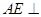
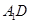 6分
6分
又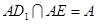 所以,
所以,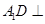 面
面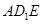
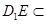 面
面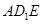 , 所以,
, 所以,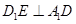 8分
8分
(3) 因为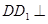 面
面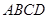 ,
,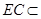 面
面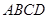 ,所以
,所以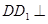
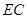 ,
,
由(1)可知,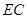
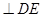 ,
, 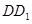
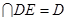
所以,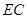
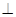 面
面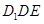 ,
10分
,
10分
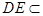 面
面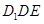 ,
, 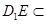 面
面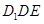
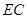
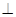
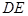 ,
,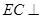
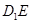
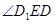 是二面角
是二面角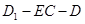 的平面角
的平面角
直角三角形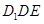 中,
中,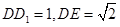
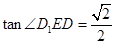
二面角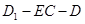 的正切值为
的正切值为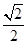 13分
13分
解法(二)

如图,以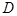 为原点,
为原点,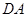 为
为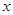 轴建立空间坐标系
轴建立空间坐标系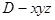
因为点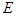 是
是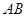 的中点,且
的中点,且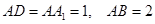
则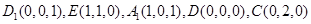
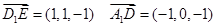 6分
6分
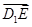

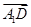 =
=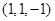

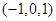
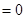
所以,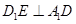 8分
8分
(3)设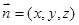 是平面
是平面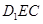 的法向量,则
的法向量,则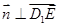 ,
,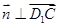
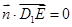 ,
,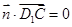 得方程组
得方程组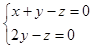 令
令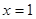 得
得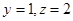
所以,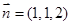 10分
10分
又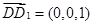 ,设
,设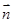 与
与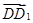 夹角为
夹角为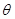
则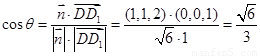
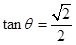
二面角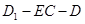 的正切值为
的正切值为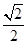 .
13分
.
13分
考点:1.勾股定理;2.三棱锥的体积;3.直线与平面的判定定理;4.向量法.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
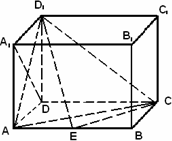
 中,
中,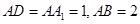 ,点E为AB的中点.
,点E为AB的中点.
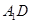 与平面
与平面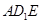 所成的角;
所成的角; 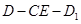 的平面角的正切值.
的平面角的正切值.