题目内容
已知函数
，
（Ⅰ）求f（x）的定义域和值域；
（Ⅱ）写出f（x）的单调区间，并用定义证明f（x）在所写区间上的单调性。
解：（Ⅰ）
，
∵
，
∴定义域为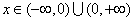
，
，
，
∴
，
∴
或
，
∴
或
，
或
，
所以，函数的值域为（-∞，-1）∪（1，+∞）。
（Ⅱ）函数f（x）的单调递减区间为（0，+∞）和（-∞，0），
设
，且
，
∴
，
∴
，
，
∴f（x）在（0，+∞）上为减函数；
同理可证，f（x）在（-∞，0）上也为减函数。
练习册系列答案
相关题目
．
．
个单位，得到函数g（x）的图象，求函数g（x）在区间[0，π]上的最大值和最小值．
．
上恒成立，求实数m的取值范围．
．
成等差数列，且
=9，求a的值．
．