题目内容
n2（n≥4,且n∈N+)个正数排成一个n列的数阵：第1列 第2列 第3列 … 第n列
第1行 a
第2行 a
第3行 a
… … … … … …
第n行 an1 an2 an3 … ann
其中aik(1≤i≤n,1≤k≤n，且i,k∈N+)表示该数阵中位于第i行第k列的数，已知该数阵每一行的数成等差数列，每一列的数成公比为2的等比数列，且a23=8,a34=20.
(1)求a11和aik;
(2)设An=a1n+a2(n-1)+a3(n-2)+…+an1,
证明：当n为3的倍数时，(An+n)能被21整除.
(1)解：设第一行公差为d,则aik=［a11+(k-1)d］×2i-1.
∵a23=8,a34=20.
∴
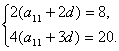解得a11=2,d=1.
∴a11=2,aik=(k+1)×2i-1(1≤i≤n,1≤k≤n，且n≥4,i,k,n∈N +).
(2)证明：∵An=a1n+a2(n-1)+a3(n-2)+…+an1
=(n+1)+n×2+(n-1)×22+…+2×2n-1,①
∴2An=(n+1)×2+n×22+(n-1)×23+…+3×2n-1+2×2n,②
②-①,得An=2+22+23+…+2n-1+2×2n-(n+1)
=2n-2+2×2n-(n+1)
=3×(2n-1)-n.
∴An+n=3×(2n-1).
下面用数学归纳法证明：当n为3的倍数时，（An+n）能被21整除.
设n=
A
（1）当m=2时，A6+6=3×(26-1)=21×9,能被21整除.∴当m=2时，结论成立.
（2）假设当m=k(k≥2)时，结论成立.
即A3k+3k=3×(23k-1)能被21整除.
当m=k+1时,
A3(k+1)+3(k+1)=3(23(k+1)-1)=3(23k×8-1)
=3(23k+7×23k-1)
=3(23k-1)+21×23k能被21整除.
∴当m=k+1时，结论成立.
由（1）（2）可知，当n为3的倍数时，An+n,能被21整除.
