题目内容
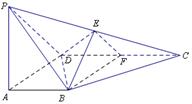
(本小题满分12分)如图,在四棱锥P-ABCD中,PA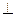 底面ABCD,
底面ABCD,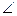 DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.
(Ⅰ)试证:AB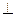 平面BEF;
平面BEF;
(Ⅱ)设PA=k ·AB,若平面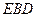 与平面
与平面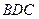 的夹角大于
的夹角大于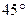 ,求k的取值范围.
,求k的取值范围.
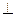 底面ABCD,
底面ABCD,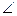 DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.(Ⅰ)试证:AB
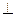 平面BEF;
平面BEF;(Ⅱ)设PA=k ·AB,若平面
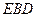 与平面
与平面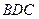 的夹角大于
的夹角大于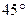 ,求k的取值范围.
,求k的取值范围.(Ⅰ)证:由已知DF∥AB且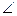 DAB为直角,故ABFD是矩形,从而AB
DAB为直角,故ABFD是矩形,从而AB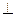 BF.
BF.
又PA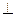 底面ABCD, 所以平面
底面ABCD, 所以平面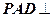 平面
平面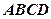 ,
,
因为AB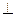 AD,故
AD,故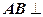 平面
平面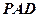 ,所以
,所以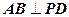 ,
,
在 内,E、F分别是PC、CD的中点,
内,E、F分别是PC、CD的中点,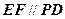 ,所以
,所以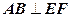 .
.
由此得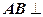 平面
平面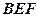 . …………6分
. …………6分
(Ⅱ)以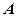 为原点,以
为原点,以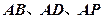 为
为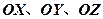 正向建立空间直角坐标系,
正向建立空间直角坐标系,
设 的长为1,则
的长为1,则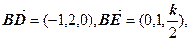
设平面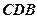 的法向量为
的法向量为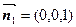 ,平面
,平面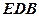 的法向量为
的法向量为 ,
,
则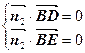
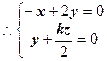 ,取
,取 ,可得
,可得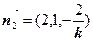
设二面角E-BD-C的大小为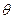 ,
,
则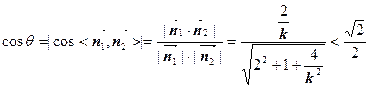
化简得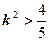 ,则
,则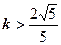 .…………12分
.…………12分
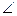 DAB为直角,故ABFD是矩形,从而AB
DAB为直角,故ABFD是矩形,从而AB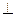 BF.
BF.又PA
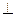 底面ABCD, 所以平面
底面ABCD, 所以平面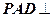 平面
平面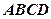 ,
,因为AB
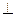 AD,故
AD,故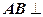 平面
平面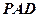 ,所以
,所以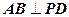 ,
,在
 内,E、F分别是PC、CD的中点,
内,E、F分别是PC、CD的中点,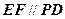 ,所以
,所以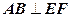 .
.由此得
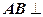 平面
平面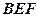 . …………6分
. …………6分(Ⅱ)以
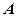 为原点,以
为原点,以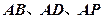 为
为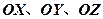 正向建立空间直角坐标系,
正向建立空间直角坐标系,
设
 的长为1,则
的长为1,则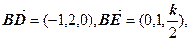
设平面
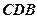 的法向量为
的法向量为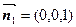 ,平面
,平面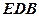 的法向量为
的法向量为 ,
,则
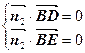
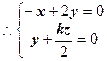 ,取
,取 ,可得
,可得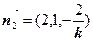
设二面角E-BD-C的大小为
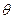 ,
,则
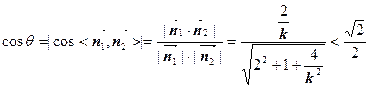
化简得
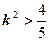 ,则
,则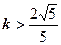 .…………12分
.…………12分略

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 平面ABCD,底面ABCD为菱形,
平面ABCD,底面ABCD为菱形, ,AB=PA=2,E.F分别为BC.PD的中点。
,AB=PA=2,E.F分别为BC.PD的中点。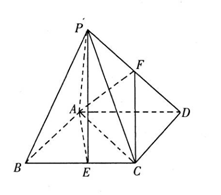
 和矩形
和矩形 所在的平面相互垂直,已知
所在的平面相互垂直,已知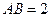 ,
,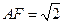 .
. 平面
平面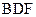 ;
;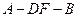 的大小.
的大小.
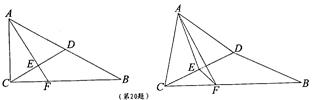
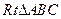 中,
中,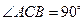 ,
,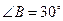 ,
,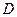 、
、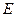 分别为
分别为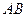 、
、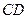 的中点,
的中点,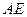 的延长线交
的延长线交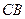 于
于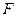 。现将
。现将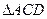 沿
沿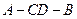 ,连接
,连接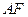 .
. :平面
:平面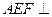 平面
平面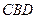 ;
;
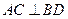 时,求二面角
时,求二面角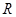 ,则这个球的内接正方体的全面积等于
,则这个球的内接正方体的全面积等于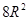
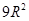
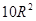
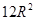
 C—E的大小。
C—E的大小。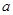 ,高为
,高为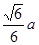 ,则此棱锥的侧面积等于( )
,则此棱锥的侧面积等于( )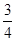
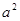
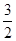
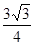

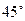 圈上有两点
圈上有两点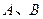 ,点
,点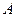 在东经
在东经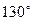 处,点
处,点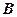 在西经
在西经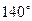 处,若地球半径为
处,若地球半径为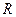 ,则
,则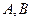 两点的球面距离为 _____________
两点的球面距离为 _____________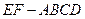 中,
中,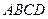 是梯形,
是梯形,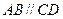 ,
,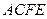 是矩形,面
是矩形,面 面
面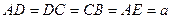 ,
,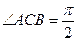 .
.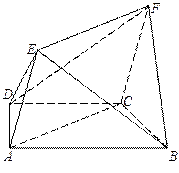
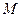 是棱
是棱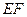 上一点,
上一点,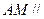 平面
平面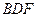 ,求
,求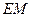 ;
;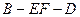 的平面角的余弦值.
的平面角的余弦值.