题目内容
O为已知圆外的定点,M在圆上,以OM为边作正三角形OMN,当点M在圆上移动时,求点N的轨迹方程(O、M、N逆时针排列).
解:以O为极点,以O和已知圆圆心O′所在射线为极轴,建立极坐标系,如图,设|OO′|=ρ0,圆的半径为r,那么圆的极坐标方程为ρ2-2ρ0ρcosθ+ρ02-r2=0,?
设N(ρ,θ),M(ρ1,θ1),?
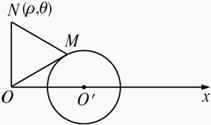
∵M在圆上,?
∴ρ12-2ρ0ρ1cosθ1+ρ02-r2=0.①?
∵△OMN为正三角形,∴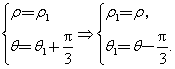
代入①得ρ2-2ρ0ρcos(θ-
)+ρ02-r2=0,这就是点N的轨迹方程.
练习册系列答案
阅读快车系列答案
相关题目
已知圆O：x2+y2=1和定点A（2，1），由圆O外一点P（a，b）向圆O引切线PQ，切点为Q，且满足|PQ|=|PA|
已知圆O：x2+y2=1和定点A（2，1），由圆外一点P（a，b）向圆O引切线PQ，切点为Q，且满足|PQ|=|PA|