题目内容
已知等差数列{an}的公差d大于0,且a2、a5是方程x2-12x+27=0的两根.数列{bn}的前n项和为Tn,满足Tn=2-bn(n∈N*).
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn,记cn=(Sn-λ)•bn(λ∈R,n∈N*).若c6为数列{cn}中的最大项,求实数λ的取值范围.
解:(Ⅰ)∵a2、a5是方程x2-12x+27=0的两根
∴a2+a5=12,a2a5=27,
∵d>0,∴a2=3,a5=9,
∴ ,
,
∴an=2n-1(n∈N*)
在已知Tn=2-bn中,令n=1,得b1=1
当n≥2时,Tn=2-bn,Tn-1=2-bn-1,两式相减得,bn=bn-1-bn,
∴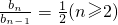 ,
,
∴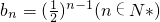
(Ⅱ)∵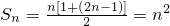 ,则
,则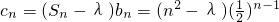
当n≥2时,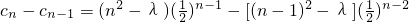 =
=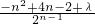
∴c6为数列{cn}中的最大项,
∴有n≥7时,cn-cn-1≤0,
∴λ≤23,n≤6时,cn-cn-1≥0,
∴λ≥14
∴14≤λ≤23.
分析:(Ⅰ)根据a2、a5是方程x2-12x+27=0的两根,可得a2+a5=12,a2a5=27,结合d>0,可得数列{an}的通项公式;利用Tn=2-bn,再写一式,两式相减,可得数列{bn}的通项公式;
(Ⅱ)根据cn=(Sn-λ)•bn,确定表达式,利用c6为数列{cn}中的最大项,即可求实数λ的取值范围.
点评:本题考查数列递推式,考查数列的通项,考查数列的单调性,确定数列的通项是关键.
∴a2+a5=12,a2a5=27,
∵d>0,∴a2=3,a5=9,
∴
 ,
,∴an=2n-1(n∈N*)
在已知Tn=2-bn中,令n=1,得b1=1
当n≥2时,Tn=2-bn,Tn-1=2-bn-1,两式相减得,bn=bn-1-bn,
∴
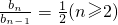 ,
,∴
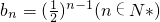
(Ⅱ)∵
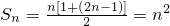 ,则
,则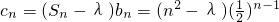
当n≥2时,
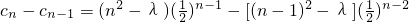 =
=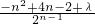
∴c6为数列{cn}中的最大项,
∴有n≥7时,cn-cn-1≤0,
∴λ≤23,n≤6时,cn-cn-1≥0,
∴λ≥14
∴14≤λ≤23.
分析:(Ⅰ)根据a2、a5是方程x2-12x+27=0的两根,可得a2+a5=12,a2a5=27,结合d>0,可得数列{an}的通项公式;利用Tn=2-bn,再写一式,两式相减,可得数列{bn}的通项公式;
(Ⅱ)根据cn=(Sn-λ)•bn,确定表达式,利用c6为数列{cn}中的最大项,即可求实数λ的取值范围.
点评:本题考查数列递推式,考查数列的通项,考查数列的单调性,确定数列的通项是关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.