题目内容
已知函数![]()
(Ⅰ)若函数 f(x)在点x=1处的切线与直线![]() 垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值;
垂直,且f(-1)=0,求函数f(x)在区间[0,3]上的最小值;
(Ⅱ)若f(x)在区间[0,1]上为单调减函数,求b的取值范围
解:(1)![]()
因为与直线![]() 垂直的直线的斜率为
垂直的直线的斜率为![]()
又f(-1)=ln(2-1)-1-4+c=0,所以c=5
f(x)=ln(x+2)-x2+4x-5,![]()
由![]()
当![]() 时,f′(x)≥0,f(x)单调递增
时,f′(x)≥0,f(x)单调递增
当![]() 时,f′(x)≤0,f(x)单调递减
时,f′(x)≤0,f(x)单调递减
又f(0)=ln2+5,f(3)=ln5+8,所以f(x)在[0,3]最小值为ln2+5
(Ⅱ)因为f(x)是减函数
所以![]() 恒成立
恒成立
因为![]() 在[0,1]上单调递增
在[0,1]上单调递增
所以(2x-![]() )min=-
)min=-![]()
所以当b≤-![]() 时,f(x)在区间[0,1]上单调递减
时,f(x)在区间[0,1]上单调递减

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
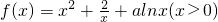 ,
,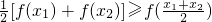 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.