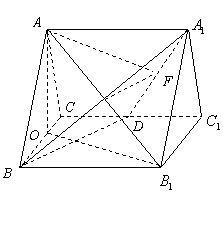
题目内容
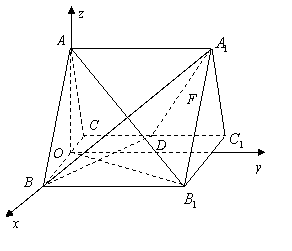
(理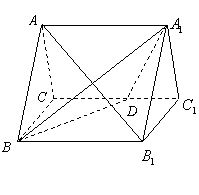 )如图,正三棱柱
)如图,正三棱柱 的所有棱长都为
的所有棱长都为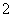 ,
, 为
为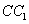 中点.
中点.
(Ⅰ)求证: 平面
平面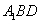 ;
;
(Ⅱ)求二面角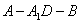 的大小;
的大小;
(Ⅲ)求点 到平面
到平面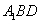 的距离.
的距离.
(文)设函数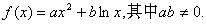
证明:当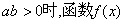 没有极值点;当
没有极值点;当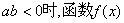 有且只有一个极值点,并求出极值
有且只有一个极值点,并求出极值
【答案】
(理)解:解法一:(Ⅰ)取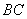 中点
中点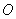 ,连结
,连结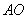 .
.
 为正三角形,
为正三角形,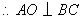 .
.
 正三棱柱
正三棱柱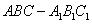 中,平面
中,平面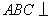 平面
平面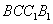 ,
,
 平面
平面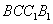 .
.
连结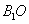 ,在正方形
,在正方形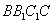 中,
中, 分别为
分别为
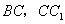 的中点,
的中点,
 ,
,
 .
.
在正方形 中,
中, ,
,
 平面
平面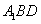 .
.
(Ⅱ)设 与
与 交于点
交于点 ,在平面
,在平面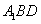 中,作
中,作 于
于 ,连结
,连结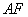 ,由(Ⅰ)得
,由(Ⅰ)得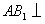 平面
平面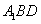 .
.
 ,
,
 为二面角
为二面角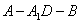 的平面角.
的平面角.
在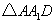 中,由等面积法可求得
中,由等面积法可求得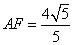 ,
,
又 ,
,
 .
.
所以二面角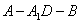 的大小为
的大小为 .
.
(Ⅲ)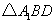 中,
中,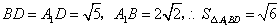 ,
,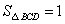 .
.
在正三棱柱中, 到平面
到平面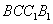 的距离为
的距离为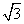 .
.
设点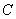 到平面
到平面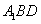 的距离为
的距离为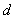 .
.
由 得
得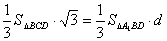 ,
,
 .
.
 点
点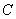 到平面
到平面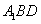 的距离为
的距离为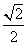 .
.
解法二:(Ⅰ)取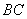 中点
中点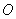 ,连结
,连结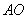 .
.
 为正三角形,
为正三角形,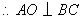 .
.
 在正三棱柱
在正三棱柱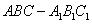 中,平面
中,平面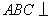 平面
平面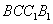 ,
,
 平面
平面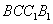 .
.
取 中点
中点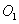 ,以
,以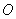 为原点,
为原点, ,
, ,
,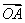 的方向为
的方向为 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则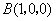 ,
, ,
, ,
,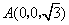 ,
,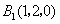 ,
,
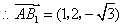 ,
, ,
, .
.
 ,
,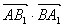 =-1+=0,
=-1+=0,
 ,
,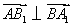 .
.
 平面
平面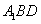 .
.
(Ⅱ)设平面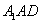 的法向量为
的法向量为 .
.
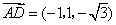 ,
,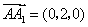 .
.
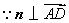 ,
, ,
,
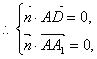
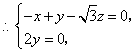

令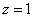 得
得 为平面
为平面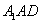 的一个法向量.
的一个法向量.
由(Ⅰ)知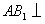 平面
平面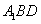 ,
,
 为平面
为平面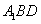 的法向量.
的法向量.
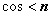 ,
, .
.
 二面角
二面角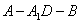 的大小为
的大小为 .
.
(Ⅲ)由(Ⅱ),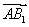 为平面
为平面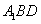 法向量,
法向量,
 .
.
 点
点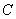 到平面
到平面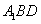 的距离
的距离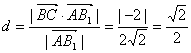 .
.
(文)证明:因为
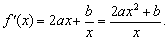
当 上单调递增;
上单调递增;
如果 上单调递增.
上单调递增.
所以当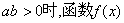 没有极值点.
没有极值点.
当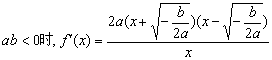 ,
,

当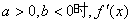 、
、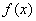 随x的变化情况如下表:
随x的变化情况如下表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
从上表可看出,
函数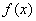 有且只有一个极小值点,
有且只有一个极小值点,
极小值为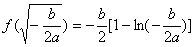 ,
,
当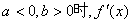 、
、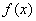 随x的变化情况如下表:
随x的变化情况如下表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
从上表可以看出,
函数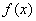 有且只一个极大值点,极大值为
有且只一个极大值点,极大值为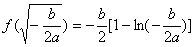 ,
,
综上所述,当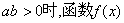 没有极值点;当
没有极值点;当 时,
时,
 有且只有一个极小值点,极大值为
有且只有一个极小值点,极大值为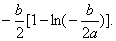
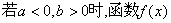 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为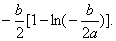

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目









