题目内容
数列{an}中,a1=1,an+1=3Sn,则{an}的通项an= .
【答案】分析:这是一道典型的含有an+1,Sn的递推公式来求通项公式的题目,利用公式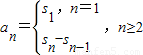 ,本题是先求出Sn,
,本题是先求出Sn,
再由Sn求出an,要注意对n=1和n≥2进行讨论.
解答:解:由已知,a1=1,an+1=3Sn=Sn+1-Sn得4Sn=Sn+1,
所以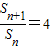 ,即{Sn}是首项为1,公比为4的等比数列,
,即{Sn}是首项为1,公比为4的等比数列,
所以Sn=1×4n-1=4n-1,
又由公式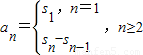 ,
,
得到an=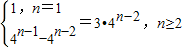 .
.
点评:本题属于基础题目,运算上较为容易,另外需注意求出Sn之后,只要注意讨论n=1和n≥2的情形,进一步求出{an}的通项公式,用到的思想方法是分段讨论法.
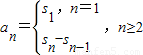 ,本题是先求出Sn,
,本题是先求出Sn,再由Sn求出an,要注意对n=1和n≥2进行讨论.
解答:解:由已知,a1=1,an+1=3Sn=Sn+1-Sn得4Sn=Sn+1,
所以
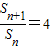 ,即{Sn}是首项为1,公比为4的等比数列,
,即{Sn}是首项为1,公比为4的等比数列,所以Sn=1×4n-1=4n-1,
又由公式
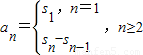 ,
,得到an=
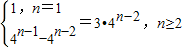 .
.点评:本题属于基础题目,运算上较为容易,另外需注意求出Sn之后,只要注意讨论n=1和n≥2的情形,进一步求出{an}的通项公式,用到的思想方法是分段讨论法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列{an}中,a1=
,an+an+1=
,n∈N*,则
(a1+a2+…+an)等于( )
| 1 |
| 5 |
| 6 |
| 5n+1 |
| lim |
| n→∞ |
A、
| ||
B、
| ||
C、
| ||
D、
|