题目内容
等差数列{an}的前项和为Sn,若a1>0,存在大于2的自然数k,使ak=Sk,则( )A.{an}递增,Sn有最大值
B.{an}递增,Sn有最小值
C.{an}递减,Sn有最大值
D.{an}递减,Sn有最小值
【答案】分析:根据所给的条件ak=Sk,用首项和公差表示出等式,因为首项是正数,所以把首项用公差和k来表示,这个表示式大于零,得到公差是一个负数,即数列是一个递减数列,sn存在最大值.
解答:解:∵ak=Sk,
∴a1+(k-1)d=ka1+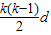 ,
,
∴a1(1-k)=(1-k)d+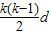
∴a1=d-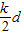 =d(1-
=d(1-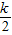 ),
),
∵a1>0,
∴d(1-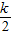 )>0,
)>0,
∵k是大于2的自然数,
∴1-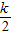 <0
<0
∴d<0,
即数列是一个递减数列,sn存在最大值,
故选C.
点评:本题没有具体的数字运算,它考查的是等差数列的性质,实际上这类问题比具体的数字运算要困难,是几个知识点结合起来的综合问题.
解答:解:∵ak=Sk,
∴a1+(k-1)d=ka1+
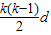 ,
,∴a1(1-k)=(1-k)d+
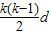
∴a1=d-
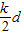 =d(1-
=d(1-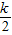 ),
),∵a1>0,
∴d(1-
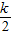 )>0,
)>0,∵k是大于2的自然数,
∴1-
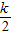 <0
<0∴d<0,
即数列是一个递减数列,sn存在最大值,
故选C.
点评:本题没有具体的数字运算,它考查的是等差数列的性质,实际上这类问题比具体的数字运算要困难,是几个知识点结合起来的综合问题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
设等差数列{an}的前n项和为Sn,则a5+a6>0是S8≥S2的( )
| A、充分而不必要条件 | B、必要而不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |