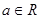题目内容
已知R上的不间断函数g(x)满足:①当x>0时,g′(x)>0恒成立;②对任意的x∈R都有g(x)=g(-x).又函数f(x)满足:对任意的x∈R,都有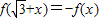 成立,当
成立,当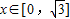 时,f(x)=x3-3x.若关于x的不等式g[f(x)]≤g(a2-a+2)对x∈[-3,3]恒成立,则a的取值范围( )
时,f(x)=x3-3x.若关于x的不等式g[f(x)]≤g(a2-a+2)对x∈[-3,3]恒成立,则a的取值范围( )A.a≤0或a≥1
B.0≤a≤1
C.-1≤a≤1
D.a∈R
【答案】分析:由于函数g(x)满足:①当x>0时,g'(x)>0恒成立(g'(x)为函数g(x)的导函数);②对任意x∈R都有g(x)=g(-x),这说明函数g(x)为R上的偶函数且在[0,+∞)上为单调递增函数,且有g|(x|)=g(x),所以g[f(x)]≤g(a2-a+2)?|f(x)|≤|a2-a+2|对x∈[-3,3]恒成立,只要使得|f(x)|在定义域内的最大值小于等于|a2-a+2|的最小值,然后解出即可.
解答:解:因为函数g(x)满足:当x>0时,g'(x)>0恒成立,
且对任意x∈R都有g(x)=g(-x),
则函数g(x)为R上的偶函数且在[0,+∞)上为单调递增函数,
且有g|(x|)=g(x),
所以g[f(x)]≤g(a2-a+2)在R上恒成立,
∴|f(x)|≤|a2-a+2|对x∈[-3,3]恒成立,
只要使得定义域内|f(x)|max≤|a2-a+2|,
由于当x∈[-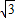 ,
,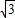 ]时,f(x)=
]时,f(x)=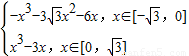 ,
,
当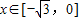 时,令f′(x)=
时,令f′(x)=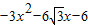 =0,得
=0,得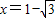 或
或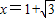 (舍去)
(舍去)
∴f(x)在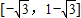 上单调递增,在
上单调递增,在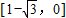 上单调递减,
上单调递减,
∴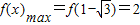 ,
,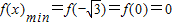 ,
,
当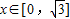 时,f′(x)=3x2-3=3(x+1)(x-1)=0,得x=1或x=-1(舍去),
时,f′(x)=3x2-3=3(x+1)(x-1)=0,得x=1或x=-1(舍去),
∴f(x)在[0,1]上单调递减,在[1,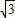 ]上单调递增,
]上单调递增,
∴f(x)min=f(1)=-2,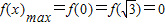 ,
,
又由于对任意的x∈R都有f(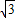 +x)=-f(x),
+x)=-f(x),
∴f(2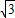 +x)=-f(
+x)=-f(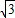 +x)=f(x)成立,则函数f(x)为周期函数且周期为T=2
+x)=f(x)成立,则函数f(x)为周期函数且周期为T=2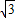 ,
,
所以函数f(x)在x∈[-3,3]的最大值为2,所以令2≤|a2-a+2|解得:a≥1或a≤0.
故选A
点评:此题考查了利用导函数求得函数在定义域上为单调递增函数,还考查了函数的周期的定义,及利用周期可以求得当x∈[-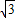 ,
,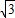 ]时,f(x)=x3-3x,的值域为[-2,2],还考查了函数恒成立.
]时,f(x)=x3-3x,的值域为[-2,2],还考查了函数恒成立.
解答:解:因为函数g(x)满足:当x>0时,g'(x)>0恒成立,
且对任意x∈R都有g(x)=g(-x),
则函数g(x)为R上的偶函数且在[0,+∞)上为单调递增函数,
且有g|(x|)=g(x),
所以g[f(x)]≤g(a2-a+2)在R上恒成立,
∴|f(x)|≤|a2-a+2|对x∈[-3,3]恒成立,
只要使得定义域内|f(x)|max≤|a2-a+2|,
由于当x∈[-
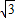 ,
,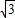 ]时,f(x)=
]时,f(x)=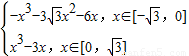 ,
,当
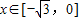 时,令f′(x)=
时,令f′(x)=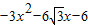 =0,得
=0,得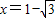 或
或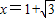 (舍去)
(舍去)∴f(x)在
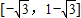 上单调递增,在
上单调递增,在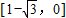 上单调递减,
上单调递减,∴
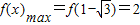 ,
,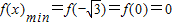 ,
,当
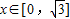 时,f′(x)=3x2-3=3(x+1)(x-1)=0,得x=1或x=-1(舍去),
时,f′(x)=3x2-3=3(x+1)(x-1)=0,得x=1或x=-1(舍去),∴f(x)在[0,1]上单调递减,在[1,
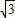 ]上单调递增,
]上单调递增,∴f(x)min=f(1)=-2,
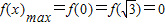 ,
,又由于对任意的x∈R都有f(
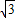 +x)=-f(x),
+x)=-f(x),∴f(2
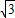 +x)=-f(
+x)=-f(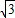 +x)=f(x)成立,则函数f(x)为周期函数且周期为T=2
+x)=f(x)成立,则函数f(x)为周期函数且周期为T=2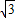 ,
,所以函数f(x)在x∈[-3,3]的最大值为2,所以令2≤|a2-a+2|解得:a≥1或a≤0.
故选A
点评:此题考查了利用导函数求得函数在定义域上为单调递增函数,还考查了函数的周期的定义,及利用周期可以求得当x∈[-
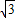 ,
,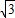 ]时,f(x)=x3-3x,的值域为[-2,2],还考查了函数恒成立.
]时,f(x)=x3-3x,的值域为[-2,2],还考查了函数恒成立. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
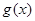 满足:①当
满足:①当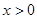 时,
时,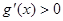 恒成立;②对任意的
恒成立;②对任意的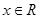 都有
都有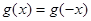 。又函数
。又函数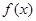 满足:对任意的
满足:对任意的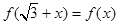 成立,当
成立,当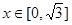 时,
时,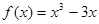 。若关于
。若关于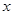 的不等式
的不等式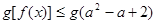 对
对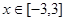 恒成立,则
恒成立,则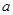 的取值范围( )
的取值范围( )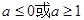 B.
B.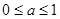 C.
C.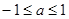 D.
D.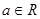
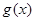 满足:①当
满足:①当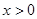 时,
时,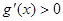 恒成立;②对任意的
恒成立;②对任意的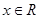 都有
都有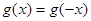 。又函数
。又函数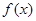 满足:对任意的
满足:对任意的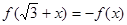 成立,当
成立,当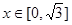 时,
时,
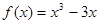 。若关于
。若关于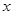 的不等式
的不等式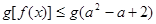 对
对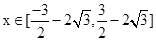 恒成立,则
恒成立,则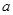 的取值范围( )
的取值范围( )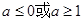 B.
B. 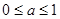 C.
C.
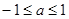 D.
D.