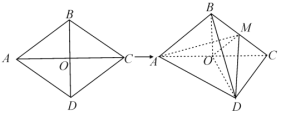
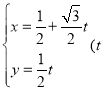��Ŀ����
����Ŀ��������![]() �뺯��
�뺯��![]() ���㣺��
���㣺��![]() ���������������ȣ���
���������������ȣ���![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() ��������
��������![]() ��ǰ
��ǰ![]() ����ĺ�
����ĺ�![]() �������
�������![]() �����������
�����������![]() ��
��![]() ���С�������ϵ����
���С�������ϵ����
��1����![]() ����д��һ��������
����д��һ��������![]() ���С�������ϵ���ĺ���
���С�������ϵ���ĺ���![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ������
������![]() ���С�������ϵ������ʵ����
���С�������ϵ������ʵ����![]() �����ɵļ��ϣ���д��
�����ɵļ��ϣ���д��![]() ����
����![]() ��
��![]() ��
��![]() �ı���ʽ��
�ı���ʽ��
��3����![]() ����֤��������ÿ�������������Ȳ�����
����֤��������ÿ�������������Ȳ�����![]() ��ʹ��
��ʹ��![]() ��
��![]() ���С�������ϵ�����ij�Ҫ�����ǡ���
���С�������ϵ�����ij�Ҫ�����ǡ���![]() ������
������![]() �ϡ���
�ϡ���
���𰸡���1��![]() ��2��ʵ����
��2��ʵ����![]() �����ɵļ���Ϊ
�����ɵļ���Ϊ![]() ����
����![]() ������
������![]() ��
�� . ��3��֤��������.
. ��3��֤��������.
��������
(1) ��![]() ����֪
����֪![]() ���Ӷ��ɵ�
���Ӷ��ɵ�![]() .
.
(2) �������![]() ,��
,��![]() ���ɵ�
���ɵ�![]() ����
����![]() ʱ����
ʱ����![]() ������������������ì��,�ʴ�ʱ�������⣻��
������������������ì��,�ʴ�ʱ�������⣻��![]() ��
��![]() ���������⣬��
���������⣬��![]() ��Ҳ��������. ��
��Ҳ��������. ��![]() ����
����![]() ����
����![]() ��
��![]() ���ɵ�
���ɵ�![]() ��
��![]() ���������������ȣ���
���������������ȣ���![]() ����֪
����֪![]() ���ó���.
����.
(3)��֤��Ҫ�ԣ���![]() ��
��![]() ����ĵȲ����У�
����ĵȲ����У�![]()
![]() ���ɵ�
���ɵ�![]() ����
���� ���
���![]() ����֤����ԣ�����
����֤����ԣ�����![]() ������
������![]() �ϣ�
�ϣ�![]()
��![]() ���ɵ�
���ɵ�![]() ���Ӷ���֤.
���Ӷ���֤.
(1)��![]() ����֪
����֪![]()
����������![]() ���С�������ϵ���ĺ���
���С�������ϵ���ĺ���![]() �Ľ���ʽ����Ϊ��
�Ľ���ʽ����Ϊ��![]() .
.
(2)�������![]() ����
����![]() ���ɵ�
���ɵ�![]() ����
����![]() .
.
����![]() ����ʱ���������������⣬
����ʱ���������������⣬
��![]() ����
����![]() ���ɵ�
���ɵ�![]() ����
����![]() ���ɵ�
���ɵ�![]() ����
����![]() ������������������ì��,�ʴ�ʱ��������.
������������������ì��,�ʴ�ʱ��������.
����![]() ���ɵ�
���ɵ�![]()
��![]() ������
������![]() ��
��![]() ���ɵ�
���ɵ�![]() ����������.
����������.
��![]() ����
����![]() ����
����![]() ʱ��
ʱ��![]() ����������.
����������.
��![]() ����
����![]() ����
����![]() ��
��![]()
�ɵ�![]() ����
����![]()
��ʱ����![]() ������Ϊ
������Ϊ![]() ������Ϊ
������Ϊ![]() �ĵȱ����У���
�ĵȱ����У���![]() ���������������ȣ�
���������������ȣ�
��![]() ����֪
����֪![]()
����ʵ����![]() �����ɵļ���Ϊ
�����ɵļ���Ϊ![]() ����
����![]() ������
������![]()

(3)(��Ҫ��)��![]() ��
��![]() ����ĵȲ����У�����
����ĵȲ����У�����![]() ���С�������ϵ��.
���С�������ϵ��.
����![]() ��
��![]()
�ɵ�: ![]()
��![]() ����
����![]() �����.
�����.
�� ���
���![]()
����![]() ,�ɵ�
,�ɵ�![]() ,
,
��![]() ,��֪
,��֪![]()
���Ե�![]() ������
������![]() ��.
��.
(�����)����![]() ������
������![]() �ϣ���
�ϣ���![]()
�ַ���![]() �ȼ���
�ȼ���![]() ��
��![]()
��![]() ��ȡ
��ȡ![]() ������Ȼ������������
������Ȼ������������![]()
��![]() ����
����![]()
![]() ��
��
�ʵ�![]() ʱ��
ʱ��![]()
������������![]() ������Ϊ
������Ϊ![]() ������Ϊ
������Ϊ![]() ������Ȳ�����.
������Ȳ�����.
����ÿһ������������Դ���ÿһ�������������Ȳ�����![]() ��ʹ��
��ʹ��![]() ��
��![]() ���С�������ϵ��.
���С�������ϵ��.