题目内容
11.已知f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$).(1)求函数y=f(x)的单调递减区间;
(2)求函数y=f(x)在x∈[0,$\frac{π}{2}$]内的值域.
分析 (1)由条件利用正弦函数的单调性求得f(x)的单调递减区间.
(2)由x∈[0,$\frac{π}{2}$],利用正弦函数的定义域和值域,求得f(x)在x∈[0,$\frac{π}{2}$]内的值域.
解答 解:(1)对于函数f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),当2kπ+$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$,k∈Z,
即kπ+$\frac{π}{8}$≤x≤kπ+$\frac{5π}{8}$,k∈Z时函数单调递增.
所以f(x)的单调递减区间为[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z.
(2)由x∈[0,$\frac{π}{2}$],知2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{4}$],从而sin(2x+$\frac{π}{4}$)∈[-$\frac{{\sqrt{2}}}{2}$,1],
故所求值域为[-1,$\sqrt{2}$].
点评 本题主要考查正弦函数的单调性、定义域和值域,属于基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
2.某中学高一年级举办了一次科普知识竞赛,该竞赛分为预赛和决赛两个阶段.预赛为笔试,决赛为面试,现将所有参赛选手参加笔试的成绩(得分均为正数,满分100分)进行统计,制成如下频率分布表.
(Ⅰ)求出上表中的x,y,z,s,p的值;
(Ⅱ)按规定,预赛成绩不低于90分的选手将参加决赛,若高一②班有甲、乙两名同学取得决赛资格,现从中选出2人担任组长,求至少有一人来自高一②班的概率.
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合计 | p | 1 |
(Ⅱ)按规定,预赛成绩不低于90分的选手将参加决赛,若高一②班有甲、乙两名同学取得决赛资格,现从中选出2人担任组长,求至少有一人来自高一②班的概率.
19. 某校对高一年级学生的数学成绩进行统计,全年级同学的成绩全部介于60分与100分之间,将他们的成绩数据绘制成如图所示的频率分布直方图.现从全体学生中,采用分层抽样的方法抽取60名同学的试卷进行分析,则从成绩在[90,100]内的学生中抽取的人数为( )
某校对高一年级学生的数学成绩进行统计,全年级同学的成绩全部介于60分与100分之间,将他们的成绩数据绘制成如图所示的频率分布直方图.现从全体学生中,采用分层抽样的方法抽取60名同学的试卷进行分析,则从成绩在[90,100]内的学生中抽取的人数为( )
 某校对高一年级学生的数学成绩进行统计,全年级同学的成绩全部介于60分与100分之间,将他们的成绩数据绘制成如图所示的频率分布直方图.现从全体学生中,采用分层抽样的方法抽取60名同学的试卷进行分析,则从成绩在[90,100]内的学生中抽取的人数为( )
某校对高一年级学生的数学成绩进行统计,全年级同学的成绩全部介于60分与100分之间,将他们的成绩数据绘制成如图所示的频率分布直方图.现从全体学生中,采用分层抽样的方法抽取60名同学的试卷进行分析,则从成绩在[90,100]内的学生中抽取的人数为( )| A. | 24 | B. | 18 | C. | 15 | D. | 12 |
6.已知数列{an}满足a1=0,an+1=$\frac{{{a_n}-2}}{{\frac{5}{4}{a_n}-2}}$,则a2015=( )
| A. | 0 | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
19.同时投掷两颗骰子,则两颗骰子向上的点数相同的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
 是定义在实数集
是定义在实数集 上的奇函数,且当
上的奇函数,且当 时,
时, 成立,若
成立,若 ,则
,则 大小关系( )
大小关系( ) B.
B.
 D.
D.
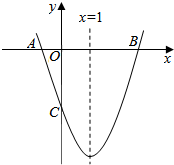 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.