题目内容
设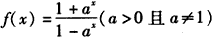 ,g(x)是f(x)的反函数。
,g(x)是f(x)的反函数。
(Ⅰ)求g(x);
(Ⅱ)当x∈[2,6]时,恒有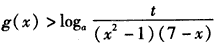 成立,求t的取值范围;
成立,求t的取值范围;
(Ⅲ)当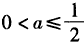 时,试比较f(1)+f(2)+…+f(n)与n+4的大小,并说明理由。
时,试比较f(1)+f(2)+…+f(n)与n+4的大小,并说明理由。
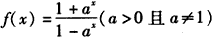 ,g(x)是f(x)的反函数。
,g(x)是f(x)的反函数。(Ⅰ)求g(x);
(Ⅱ)当x∈[2,6]时,恒有
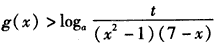 成立,求t的取值范围;
成立,求t的取值范围;(Ⅲ)当
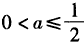 时,试比较f(1)+f(2)+…+f(n)与n+4的大小,并说明理由。
时,试比较f(1)+f(2)+…+f(n)与n+4的大小,并说明理由。解:(Ⅰ)由题意得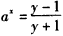
故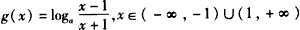 ;
;
(Ⅱ)由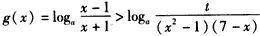 得
得
①当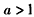 时,
时,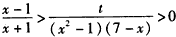
又因为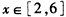
所以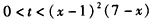
令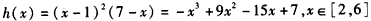
则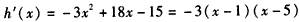
列表如下:
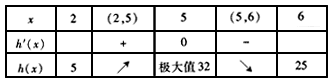
所以h(x)最小值=5,所以0<t<5
当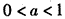 时,
时,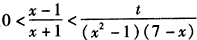
又因为x∈ [2,6]
所以t>(x-1)2(7-x)>0
令h(x)=(x-1)2(7-x),x∈[2,6],
由①知h(x)最大值=32
所以t>32
综上,当a>1时,0<t<5
当0<a<1时,t>32。
(Ⅲ)设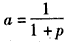 ,则
,则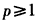
当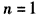 时,
时,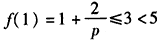
当n≥2时,设k≥2,k∈N*时
则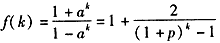
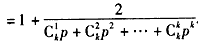
所以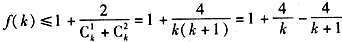
从而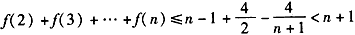
所以f(1)+f(2)+…+f(n)<f(1)+n+1≤n+4
综上,总有,f(1)+f(2)+…+f(n)< n+4。
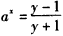
故
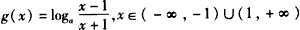 ;
;(Ⅱ)由
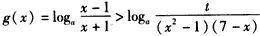 得
得①当
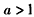 时,
时,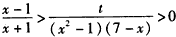
又因为
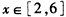
所以
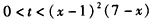
令
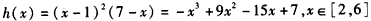
则
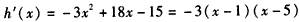
列表如下:

所以h(x)最小值=5,所以0<t<5
当
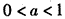 时,
时,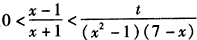
又因为x∈ [2,6]
所以t>(x-1)2(7-x)>0
令h(x)=(x-1)2(7-x),x∈[2,6],
由①知h(x)最大值=32
所以t>32
综上,当a>1时,0<t<5
当0<a<1时,t>32。
(Ⅲ)设
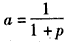 ,则
,则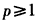
当
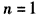 时,
时,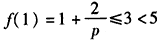
当n≥2时,设k≥2,k∈N*时
则
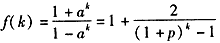
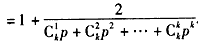
所以
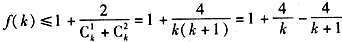
从而
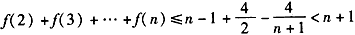
所以f(1)+f(2)+…+f(n)<f(1)+n+1≤n+4
综上,总有,f(1)+f(2)+…+f(n)< n+4。

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目