题目内容
已知中心在坐标原点O的椭圆C经过点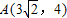 ,点
,点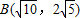 .
.(1)求椭圆C的方程;
(2)已知圆M:x2+(y-5)2=9,双曲线G与椭圆C有相同的焦点,它的两条渐近线恰好与圆M相切,求双曲线G的方程.
【答案】分析:(1)待定系数法求椭圆的方程,设椭圆C的方程为mx2+ny2=1,将点 ,点
,点 代入,建立方程组,即可求出椭圆C的方程;
代入,建立方程组,即可求出椭圆C的方程;
(2)设出双曲线方程,利用圆M:x2+(y-5)2=9,双曲线G与椭圆C有相同的焦点,它的两条渐近线恰好与圆M相切,建立两个方程,从而可求出双曲线G的方程.
解答:解:(1)依题意,可设椭圆C的方程为mx2+ny2=1,…(1分)
从而 ,解得
,解得 …(3分)
…(3分)
故椭圆C的方程为 …(4分)
…(4分)
(2)椭圆C: 的两焦点为F1(-5,0),F2(5,0),…(5分)
的两焦点为F1(-5,0),F2(5,0),…(5分)
∵双曲线G与椭圆C有相同的焦点,
∴双曲线的中心在原点,焦点在x轴上,且c=5.…(6分)
设双曲线G的方程为 (a>0,b>0),则G的渐近线方程为y=±
(a>0,b>0),则G的渐近线方程为y=± x,…(7分)
x,…(7分)
即bx±ay=0,且a2+b2=25,
圆M:x2+(y-5)2=9的圆心为(0,5),半径为r=3.
∵双曲线G的两条渐近线恰好与圆M相切
∴
∴a=3,b=4.…(9分)
∴双曲线G的方程为 .…(10分)
.…(10分)
点评:本题考查椭圆、双曲线的标准方程,考查待定系数法,根据不同条件,设出方程是我们解答这类问题的关键.
 ,点
,点 代入,建立方程组,即可求出椭圆C的方程;
代入,建立方程组,即可求出椭圆C的方程;(2)设出双曲线方程,利用圆M:x2+(y-5)2=9,双曲线G与椭圆C有相同的焦点,它的两条渐近线恰好与圆M相切,建立两个方程,从而可求出双曲线G的方程.
解答:解:(1)依题意,可设椭圆C的方程为mx2+ny2=1,…(1分)
从而
 ,解得
,解得 …(3分)
…(3分)故椭圆C的方程为
 …(4分)
…(4分)(2)椭圆C:
 的两焦点为F1(-5,0),F2(5,0),…(5分)
的两焦点为F1(-5,0),F2(5,0),…(5分)∵双曲线G与椭圆C有相同的焦点,
∴双曲线的中心在原点,焦点在x轴上,且c=5.…(6分)
设双曲线G的方程为
 (a>0,b>0),则G的渐近线方程为y=±
(a>0,b>0),则G的渐近线方程为y=± x,…(7分)
x,…(7分)即bx±ay=0,且a2+b2=25,
圆M:x2+(y-5)2=9的圆心为(0,5),半径为r=3.
∵双曲线G的两条渐近线恰好与圆M相切
∴

∴a=3,b=4.…(9分)
∴双曲线G的方程为
 .…(10分)
.…(10分)点评:本题考查椭圆、双曲线的标准方程,考查待定系数法,根据不同条件,设出方程是我们解答这类问题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目