题目内容
【题目】一青蛙从点
开始依次水平向右和竖直向上跳动，其落点坐标依次是
，（如图所示，坐标以已知条件为准），
表示青蛙从点
到点
所经过的路程.
（1）若点为抛物线
（
）准线上一点，点
均在该抛物线上，并且直线经过该抛物线的焦点，证明
.
（2）若点
要么落在
所表示的曲线上，要么落在
所表示的曲线上，并且
,试写出
（不需证明）；
（3）若点要么落在
所表示的曲线上，要么落在
所表示的曲线上，并且
，求的表达式.
【答案】解：(1)设
，由于青蛙依次向右向上跳动，
所以
，
，由抛物线定义知：
分
(2) 依题意，
随着
的增大，点
无限接近点
分
横向路程之和无限接近
，纵向路程之和无限接近
分
所以
=
分
(3)方法一：设点
，由题意，的坐标满足如下递推关系：
，且
其中
分
∴
，即
，
∴
是以
为首项，
为公差的等差数列，
∴
，
所以当为偶数时，
，于是
，
又
∴当为奇数时，
分
当为偶数时，
当为奇数时，
所以，当为偶数时，
当为奇数时，
所以，
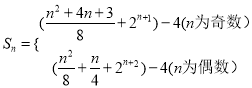
分
方法二：由题意知
其中
观察规律可知：下标为奇数的点的纵坐标为首项为
，公比为
的等比数列．相邻横坐标之差为首项为2，公差为1的等差数列．下标为偶数的点也有此规律．并由数学归纳法可以证明．
分
所以，当为偶数时，
当为奇数时，
当为偶数时，
当为奇数时，分
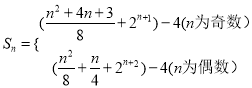
所以，分
【解析】
试题（1）直接借助题设求解即可获证；（2）运用题设条件和极限思想表示出来再求解即可；（3）运用题设中提供的信息分类进行求解．
试题解析：（1）设
，由于青蛙依次向右向上跳动，
所以
，
，由抛物线定义知：．
（2）依题意，
，
，
（
）
随着的增大，点无限接近点
，
横向路程之和无限接近，纵向路程之和无限接近，
所以
．
（3）方法一：设点
，则题意，的坐标满足如下递推关系：
，且
，
（
）
其中
，
∴，即，
∴是以为首项，2为公差的等差数列，
∴，
所以当为偶数时，，于是，
又，
∴当为奇数时，
，
，
当为偶数时，
当为奇数时，
所以，当为偶数时，
当为奇数时，
所以，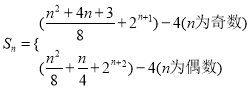
．
方法二：由题意知
，
，
，
，
，
，…
其中，，，
，…
，，，
…
观察规律可知：下标为奇数的点的纵坐标为首项为，公比为4的等比数列，相邻横坐标之差为首项为2，公差为1的等差数列，下标为偶数的点也有此规律，并由数学归纳法可以证明．
所以，当为偶数时，
当为奇数时，
，
当为偶数时，
当为奇数时，
所以，．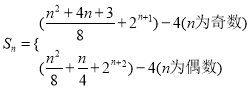
