Question

求正四面体的内切球与外接球的半径之比.

      

Answer 1

解析：方法一：如图所示，设四面体的棱长为a，球心为O，OA=R为外接圆的半径，OO₁=r为内切圆的半径，M是BC的中点，显然O₁是底面BCD的中心，AO₁⊥底面BCD，过O作ON⊥AM于点N.?

       ∵BC⊥DM,BC⊥AM,∴BC⊥ADM.又∵ON平面ADM，∴BC⊥ON,ON⊥平面ABC,即ON=r.?

       在Rt△AON中，sin∠MAO=.?

       在Rt△AO₁M中，sin∠MAO=，?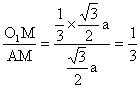

       即内切球与外接球的半径之比为1∶3.?

       方法二：如图所示，在Rt△AO₁M中，?

       AO₁=,?

       ∴V_A—BCD=×S_△BCD×AO₁=× a²×a=.??

       又∵V _A—BCD=V _O—ABC+V_O—ABD+V_O—ACD+V_O—BCD=rS_全，?

       r=,?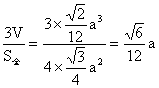

       ∴R=AO₁-r=,即R∶r=3∶1.