题目内容
11.已知定义在R上函数f(x)部分自变量与函数值对应关系如表,若f(x)为偶函数,且在[0,+∞)上为增函数,不等式1<f(x-1)<2的解集是( )| x | 0 | 2 | 3 | 4 |
| f(x) | -1 | 1 | 2 | 3 |
| A. | (-2,-1) | B. | (3,4) | C. | (-2,-1)∪(3,4) | D. | (-2,4) |
分析 根据函数奇偶性和单调性之间的关系先求出1<f(x)<2的解集即可得到结论.
解答 解:∵f(x)为偶函数,且在[0,+∞)上为增函数,
∴不等式1<f(x)<2等价为1<f(|x|)<2,
由表格知,2<|x|<3,即2<x<3或-3<x<-2,
由2<x-1<3或-3<x-1<-2,
得3<x<4或-2<x<-1,
即不等式1<f(x-1)<2的解集是(-2,-1)∪(3,4),
故选:C
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性之间的关系先求出1<f(x)<2的解集是解决本题的关键.

练习册系列答案
相关题目
19.已知曲线f(x)=lnx在点(x0,f(x0))处的切线经过点(0,-1),则x0的值为( )
| A. | $\frac{1}{e}$ | B. | 1 | C. | e | D. | 10 |
6.m,n,l是直线,α,β是两个不同的平面,下面说法正确的是( )
| A. | 若m∥α,m∥β,则α∥β | |
| B. | 若m⊥α,m?β,则α⊥β | |
| C. | 若m?α,n?α,m,n是异面直线,则n与α相交 | |
| D. | 若m?α,n?α,l⊥m,l⊥n,则l⊥α |
16.根据下面某工程工作明细表,完成第(1)、(2)题.
(1)完成下表,画出网络图.
(2)根据第(1)题表画出该工程横道图.
| 工作代码 | 工期/天 | 紧前工作 |
| A | 5 | 无 |
| B | 1 | A |
| C | 6 | A |
| D | 2 | A |
| E | 3 | B、C |
| F | 4 | B、C |
| 工作代码 | 工期/天 | 紧前工作 | 紧后工作 |
| A | 5 | 无 | |
| B | 1 | A | |
| C | 6 | A | |
| D | 2 | A | |
| E | 3 | B、C | |
| F | 4 | B、C |

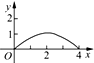
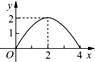
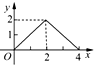
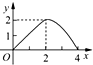
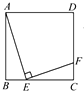 如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )
如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )