题目内容
已知函数
，
．
（1）当
时，若
上单调递减，求a的取值范围；
（2）求满足下列条件的所有整数对
：存在
，使得
的最大值，
的最小值；
（1）当时，
， ………………………………………1分
若
，
，则
在
上单调递减，符合题意；………3分
若
，要使在上单调递减，
必须满足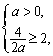
………………………………#k#s5u……………………5分
∴
．综上所述，a的取值范围是
…………………………………6分
（2）若，
，则无最大值， 故，∴为二次函数，
要使有最大值，必须满足
即
且
， …………………………………………8分
此时，
时，有最大值． ………………………………………9分
又
取最小值时，
， ………………………………………………………10分
依题意，有
，则
， …………11分
∵且，∴
，得
， ………………12分
此时
或
．
∴满足条件的整数对
是
． ……………………………13分
练习册系列答案
巧学巧练系列答案
课课练江苏系列答案
相关题目