题目内容
已知函数f(x)=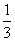 x3-bx2+2x+a,x=2是f(x)的一个极值点,
x3-bx2+2x+a,x=2是f(x)的一个极值点,
(Ⅰ)求b的值和f(x)的单调递增区间;
(Ⅱ)若当x∈[1,3]时,f(x)-a2>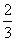 恒成立,求a的取值范围.
恒成立,求a的取值范围.
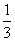 x3-bx2+2x+a,x=2是f(x)的一个极值点,
x3-bx2+2x+a,x=2是f(x)的一个极值点,(Ⅰ)求b的值和f(x)的单调递增区间;
(Ⅱ)若当x∈[1,3]时,f(x)-a2>
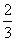 恒成立,求a的取值范围.
恒成立,求a的取值范围.解:(Ⅰ)f′(x)=x2-2bx+2,
∵x=2是f(x)的一个极值点,
∴x=2是方程x2-2bx+2=0的一个根,解得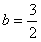 ,
,
令f′(x)>0,则x2-3x+2>0,解得x<1或x>2,
∴函数y=f(x)的单调递增区间为(-∞,1),(2,+∞)。
(Ⅱ)∵当x∈(1,2)时,f′(x)<0,当x∈(2,3)时,f′(x)>0,
∴f(x)在(1,2)上单调递减,f(x)在(2,3)上单调递增,
∴f(2)是f(x)在区间[1,3]上的最小值,且f(2)=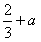 ,
,
若当x∈[1,3]时,要使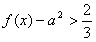 恒成立,
恒成立,
只需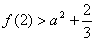 ,
,
即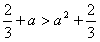 ,解得0<a<1。
,解得0<a<1。
∵x=2是f(x)的一个极值点,
∴x=2是方程x2-2bx+2=0的一个根,解得
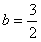 ,
,令f′(x)>0,则x2-3x+2>0,解得x<1或x>2,
∴函数y=f(x)的单调递增区间为(-∞,1),(2,+∞)。
(Ⅱ)∵当x∈(1,2)时,f′(x)<0,当x∈(2,3)时,f′(x)>0,
∴f(x)在(1,2)上单调递减,f(x)在(2,3)上单调递增,
∴f(2)是f(x)在区间[1,3]上的最小值,且f(2)=
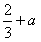 ,
,若当x∈[1,3]时,要使
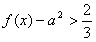 恒成立,
恒成立,只需
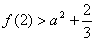 ,
,即
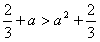 ,解得0<a<1。
,解得0<a<1。
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目