题目内容
16.在△ABC中,角A,B,C的对边分别为a,b,c,已知bsinA+a(cosB-$\sqrt{2}$)=0.(1)求角B的大小;
(2)若△ABC的面积为3,a+c=3+2$\sqrt{2}$,求b.
分析 (1)由正弦定理结合sinA≠0,化简可得:sin(B+$\frac{π}{4}$)=1,结合0<B<π,可解得B的值.
(2)由△ABC的面积为3=$\frac{1}{2}$acsinB,整理可得:ac=6$\sqrt{2}$,利用余弦定理即可解得b的值.
解答 解:(1)∵bsinA+a(cosB-$\sqrt{2}$)=0,
∴由正弦定理可得:sinBsinA+sinA(cosB-$\sqrt{2}$)=0,
∴由于sinA≠0,可得:sinB+cosB=$\sqrt{2}$,即:$\sqrt{2}$sin(B+$\frac{π}{4}$)=$\sqrt{2}$,
∴sin(B+$\frac{π}{4}$)=1,
∴结合0<B<π,可得:B+$\frac{π}{4}$=$\frac{π}{2}$,从而解得:B=$\frac{π}{4}$.
(2)∵△ABC的面积为3,a+c=3+2$\sqrt{2}$,
∴由△ABC的面积为3=$\frac{1}{2}$acsinB,整理可得:ac=6$\sqrt{2}$.
∴由余弦定理可得:b2=a2+c2-2accosB=$(a+c)^{2}-2ac-\sqrt{2}ac$=(3+2$\sqrt{2}$)2-2×$6\sqrt{2}$-$\sqrt{2}×6\sqrt{2}$=5.
∴解得:b=$\sqrt{5}$.
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式的应用,属于基本知识的考查.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
15.复数z1、z2在复平面内的对应点关于原点对称,且z1=2+i,则$\frac{({z}_{1}-1)^{2}}{|{z}_{2}+1|}$等于( )
| A. | $\sqrt{2}$i | B. | $\frac{\sqrt{10}}{5}$i | C. | $\sqrt{2}$ | D. | 4$\sqrt{2}$+3$\sqrt{2}$i |
1.已知函数f(x)=$\frac{1}{2}$cos(2x+$\frac{5π}{6}$),则y=f(x)的图象可由函数g(x)=$\frac{1}{2}$sin(x+$\frac{π}{2}$)的图象(纵坐标不变)( )
| A. | 先把各点的横坐标缩短到原来的$\frac{1}{2}$倍,再向右平移$\frac{5π}{12}$个单位 | |
| B. | 先把各点的横坐标伸长到原来的2倍,再向右平移$\frac{5π}{6}$个单位 | |
| C. | 先把各点的横坐标缩短到原来的$\frac{1}{2}$倍,再向左平移$\frac{5π}{12}$个单位 | |
| D. | 先把各点的横坐标伸长到原来的2倍,再向左平移$\frac{5π}{6}$个单位 |
5.在下列各图中,图中两个变量具有相关关系的图是( )
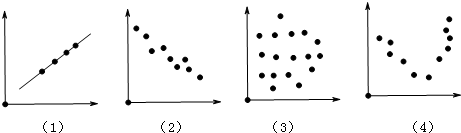

| A. | (1)(2) | B. | (1)(4) | C. | (2)(4) | D. | (2)(3) |