题目内容
【题目】如图，已知椭圆C1： 
+y2=1，双曲线C2： 
=1（a＞0，b＞0），若以C1的长轴为直径的圆与C2的一条渐近线交于A，B两点，且C1与该渐近线的两交点将线段AB三等分，则C2的离心率为（ ）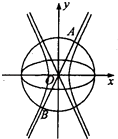 
A.
B.5
C.
D.
【答案】A
【解析】解：双曲线C2： 
=1（a＞0，b＞0）的一条渐近线方程为 y= 
x，
以C1的长轴为直径的圆的方程为x2+y2=11，
联立渐近线方程和圆的方程，可得交点A（ 
， 
），B（﹣ ，﹣ ），
联立渐近线方程和椭圆C1： 
+y2=1，可得交点C（ 
， 
），
D（﹣ ，﹣ ），
由于C1与该渐近线的两交点将线段AB三等分，
则|AB|=3|CD|，
即有 
= 
，化简可得，b=2a，
则c= 
= 
a，
则离心率为e= 
= ．
故选A．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
