题目内容
(2012•宜宾一模)设f(x)等于(x2+
) 6展开式的中间项,若f(x)≤mx在区间[
,
]上恒成立,则m的取值范围是( )
| 1 |
| 2x |
| ||
| 2 |
| 2 |
分析:先由二项式定理可以得到(x2+
) 6展开式的通项,再求出其展开式的中间项,即可得f(x),由x的范围,可将f(x)≤mx变形为
x2≤m,由二次函数的性质,求出
x2在区间[
,
]上的最大值,结合不等式恒成立的意义,即可得答案.
| 1 |
| 2x |
| 5 |
| 2 |
| 5 |
| 2 |
| ||
| 2 |
| 2 |
解答:解:(x2+
) 6展开式的通项为Tr+1=C6r(x2)6-r(
)r=(
)r•C6r•x12-3r,
其展开式的中间项为T4=(
)3•C63•x3=
x3,即f(x)=
x3,
f(x)≤mx?
x3≤mx,
当
≤x≤
时,
x3≤mx?
x2≤m,
且
≤x≤
时,
x2的最大值为5,则若
x2≤m恒成立,则必有m≥5,
故m的取值范围是[5,+∞),
故选A.
| 1 |
| 2x |
| 1 |
| 2x |
| 1 |
| 2 |
其展开式的中间项为T4=(
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
f(x)≤mx?
| 5 |
| 2 |
当
| ||
| 2 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
且
| ||
| 2 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
故m的取值范围是[5,+∞),
故选A.
点评:本题考查二项式定理与函数的恒成立问题,关键由二项式定理求出f(x)并求出其最大值.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
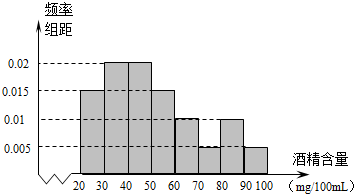 (2012•宜宾一模)《中华人民共和国道路交通安全法》
(2012•宜宾一模)《中华人民共和国道路交通安全法》