题目内容
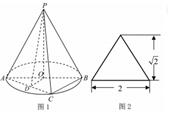
如图,已知 平面
平面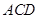 ,
, ,
, ,
,
且 是
是 的中点,
的中点, .
.
(1)求证: 平面
平面 ;
;
(2)求证:平面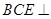 平面
平面 ;
;
(3)求此多面体的体积.
(1)详见解析;(2)详见解析;(3)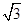 .
.
解析试题分析:(1)取 的中点
的中点 ,连结
,连结 、
、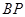 ,利用中位线证明
,利用中位线证明 ,利用题中条件得到
,利用题中条件得到 ,进而得到
,进而得到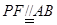 ,于是说明四边形
,于是说明四边形 为平行四边形,得到
为平行四边形,得到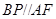 ,最后利用直线与平面平行的判定定理证明
,最后利用直线与平面平行的判定定理证明 平面
平面 ;(2)由
;(2)由 平面
平面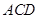 得到
得到 ,再利用等腰三角形三线合一得到
,再利用等腰三角形三线合一得到 ,利用直线与平面垂直的判定定理证明
,利用直线与平面垂直的判定定理证明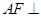 平面
平面 ,结合(1)中的结论
,结合(1)中的结论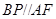 证明
证明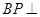 平面
平面 ,最后利用平面与平面垂直的判定定理证明平面
,最后利用平面与平面垂直的判定定理证明平面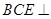 平面
平面 ;(3)利用已知条件得到平面
;(3)利用已知条件得到平面 平面
平面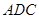 ,然后利用平面与平面垂直的性质定理求出椎体
,然后利用平面与平面垂直的性质定理求出椎体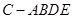 的高,最后利用椎体的体积公式计算该几何体的体积.
的高,最后利用椎体的体积公式计算该几何体的体积.
(1)取 中点
中点 ,连结
,连结 、
、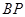 ,
,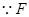 为
为 的中点,
的中点,  ,且
,且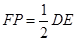 ,
,
又 ,且
,且
 ,且
,且 ,
,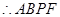 为平行四边形,
为平行四边形, ,
,
又 平面
平面 ,
, 平面
平面 ,
,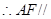 平面
平面 ;
;
(2) ,
,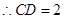 ,所以
,所以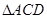 为正三角形,
为正三角形,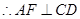 ,
, 平面
平面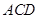 ,
, ,
, 平面
平面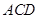 ,又
,又 平面
平面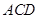 ,
, ,又
,又 ,
,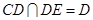 ,
,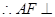 平面
平面 ,又
,又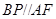 ,
,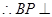 平面
平面 ,
,
又 平面
平面 ,
, 平面
平面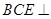 平面
平面 ;
;
(3)此多面体是一个以 为定点,以四边形
为定点,以四边形 为底边的四棱锥,
为底边的四棱锥,
练习册系列答案
相关题目
 1.
1. 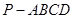 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中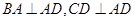 ,
, ,平面
,平面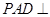 底面
底面 是
是 的中点.
的中点.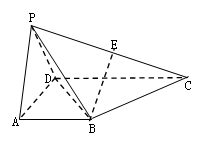
 //平面
//平面 ;
;
 ;
;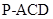 的体积
的体积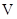 .
.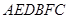 的直观图及三视图如图所示,
的直观图及三视图如图所示,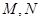 分别为
分别为 的中点.
的中点. 平面
平面 ;
; 的体积.
的体积.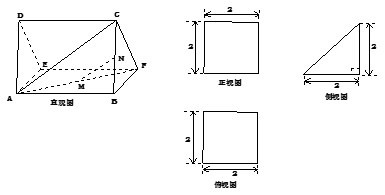
 ,其表面展开图是三角形
,其表面展开图是三角形 ,如图,求△
,如图,求△ .
.
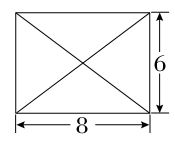
 中,
中, ,
, ,
, °,平面
°,平面 平面
平面 ,
, ,
, 分别为
分别为 ,
, 中点.
中点. ∥平面
∥平面 ;
; ;
; 的体积.
的体积.
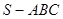 中,
中,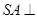 底面
底面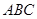 ,
,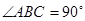 ,且
,且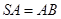 ,
,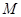 是
是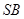 的中点,
的中点,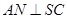 且交
且交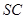 于点
于点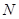 .
.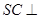 平面
平面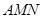 ;
;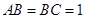 时,求三棱锥
时,求三棱锥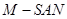 的体积.
的体积.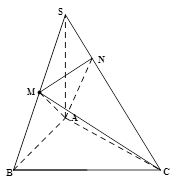
 平面POD;
平面POD; ,在三棱锥A-PBC中,求点A到平面PBC的距离.
,在三棱锥A-PBC中,求点A到平面PBC的距离.