Question

【题目】如图，在三棱柱ABC﹣A1B1C1中，面ABB1A1为矩形，AB=1，AA1= ，D为AA1的中点，BD与AB1交于点O，CO⊥面ABB1A1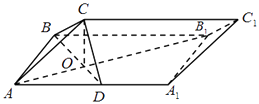
（Ⅰ）证明：BC⊥AB1
（Ⅱ）若OC=OA，求二面角A﹣BC﹣B1的余弦值．

Answer 1

【答案】（Ⅰ）证明：由△AB1B与△DBA相似，知DB⊥AB1，

又CD⊥平面ABB1A1，∴CD⊥AB1，

∴AB1⊥平面BDC，∴AB1⊥BC．

（Ⅱ）解：以O为坐标原点，OA、OD、OC所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，

则A（ ，0，0），B（0，﹣ ，0），C（0，0， ），B1（﹣ ，0，0），

=（0， ， ）， =（﹣ ，﹣ ，0）， =（﹣ ， ，0），

设平面ABC，平面BCB1的法向量分别为 ，

则 ，取x= ，得 =（ ），

，取a=1，得 =（1， ，﹣2），

∴cos＜ ＞= = ，

∴二面角A﹣BC﹣B1的余弦值为﹣ ．

【解析】（Ⅰ）推导出DB⊥AB1，CD⊥AB1，从而AB1⊥平面BDC，由此能证明AB1⊥BC．（Ⅱ）以O为坐标原点，OA、OD、OC所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，利用向量法能求出二面角A﹣BC﹣B1的余弦值．
【考点精析】认真审题，首先需要了解空间中直线与直线之间的位置关系(相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点)．