题目内容
已知函数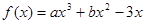 在
在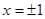 处取得极值,求函数
处取得极值,求函数 以及
以及 的极大值和极小值.
的极大值和极小值.
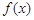 在
在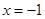 处取得极大值
处取得极大值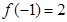 ,在
,在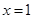 处取得极小值
处取得极小值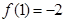 .
.
解析试题分析:先求出导函数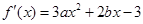 ,进而根据条件得出
,进而根据条件得出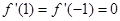 ,列出方程组
,列出方程组 ,从中解出
,从中解出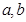 的值,进而根据函数的极值与导数的关系求解出函数
的值,进而根据函数的极值与导数的关系求解出函数 的极大值与极小值即可.
的极大值与极小值即可.
试题解析:因为 ,所以
,所以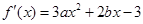
因为函数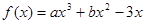 在
在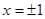 处取得极值
处取得极值
所以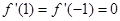
即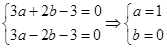
∴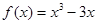 ,
,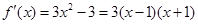
令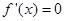 ,得
,得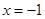 或
或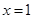
当 变化时,
变化时,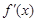 与
与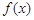 的变化情况如下表:
的变化情况如下表: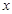
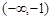
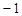
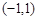
1 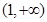
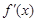
+ 0 — 0 + 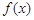
↗ 极大值 ↘ 极小值 ↗
∴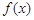 在
在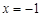 处取得极大值
处取得极大值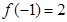 ,在
,在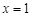 处取得极小值
处取得极小值

练习册系列答案
相关题目
 对称,且f′(1)=0.
对称,且f′(1)=0.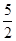 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+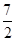 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数). ,
,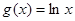 .
. 的极值;(2)若
的极值;(2)若 恒成立,求实数
恒成立,求实数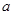 的值;
的值;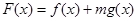
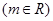 有两个极值点
有两个极值点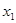 、
、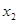 (
(
 的取值范围,并证明
的取值范围,并证明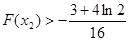 .
.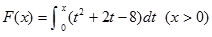 .
. 的单调区间;(2)求函数
的单调区间;(2)求函数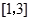 上的最值.
上的最值.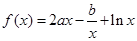 在
在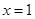 与
与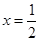 处都取得极值.
处都取得极值.  ,
,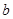 的值;
的值;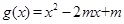 ,若对任意的
,若对任意的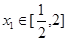 ,总存在
,总存在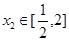 ,使得、
,使得、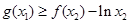 ,求实数
,求实数 的取值范围.
的取值范围.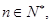 圆
圆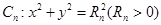 与
与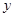 轴正半轴的交点为
轴正半轴的交点为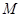 ,与曲线
,与曲线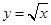 的交点为
的交点为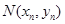 ,直线
,直线 与
与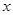 轴的交点为
轴的交点为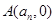 .
. 表示
表示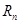 和
和
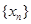 满足
满足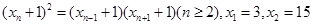
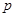 的值,使得数列
的值,使得数列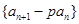 成等比数列;
成等比数列;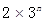 的大小.
的大小.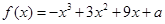 ,
,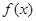 的单调递减区间;
的单调递减区间;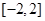 上的最大值为20,求它在该区间上的最小值.
上的最大值为20,求它在该区间上的最小值.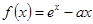 (
( 为常数)的图象与
为常数)的图象与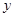 轴交于点
轴交于点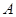 ,曲线
,曲线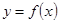 在点
在点 的极值;
的极值;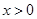 时,
时,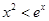 ;
;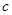 ,总存在
,总存在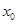 ,使得当
,使得当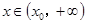 ,恒有
,恒有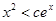 .
.