题目内容
下列命题中,真命题的序号有
①当x>0且x≠1时,有lnx+
≥2;
②函数f(x)=lg(ax+1)的定义域是{x|x>-
};
③函数f(x)=e-xx2在x=2处取得极大值;
④若sin(α+β)=
,sin(α-β)=
,则tanαcotβ=5.
③④
③④
.(写出所有真命题的序号)①当x>0且x≠1时,有lnx+
| 1 |
| lnx |
②函数f(x)=lg(ax+1)的定义域是{x|x>-
| 1 |
| a |
③函数f(x)=e-xx2在x=2处取得极大值;
④若sin(α+β)=
| 1 |
| 2 |
| 1 |
| 3 |
分析:通过特例判断①的正误;通过a的符号判断②的正误;利用导数与极值的关系判断③的正误;利用两角和与差的三角函数计算④判断正误即可.
解答:解:对于①当x>0且x≠1时,有lnx+
≥2,不正确,例如x=
,左侧是负数,不正确;
对于②函数f(x)=lg(ax+1)可知ax>-1,当a>0时函数的定义域是{x|x>-
};a<0时函数的定义域是{x|x<-
};
所以②不正确;
对于③函数f(x)=e-xx2,f′(x)=-e-xx2+2e-xx,令-e-xx2+2e-xx,解得x=2,
当x<2时导函数f′(x)>0,函数是增函数,
当x>2时f′(x)<0,函数是奇函数,
所以函数在x=2处取得极大值;正确.
对于④若sin(α+β)=
=sinαcosβ+cosαsinβ,
sin(α-β)=
=sinαcosβ-cosαsinβ,
解得sinαcosβ=
,cosαsinβ=
,
∴tanαcotβ=5,正确.
故答案为:③④.
| 1 |
| lnx |
| 1 |
| 2 |
对于②函数f(x)=lg(ax+1)可知ax>-1,当a>0时函数的定义域是{x|x>-
| 1 |
| a |
| 1 |
| a |
所以②不正确;
对于③函数f(x)=e-xx2,f′(x)=-e-xx2+2e-xx,令-e-xx2+2e-xx,解得x=2,
当x<2时导函数f′(x)>0,函数是增函数,
当x>2时f′(x)<0,函数是奇函数,
所以函数在x=2处取得极大值;正确.
对于④若sin(α+β)=
| 1 |
| 2 |
sin(α-β)=
| 1 |
| 3 |
解得sinαcosβ=
| 5 |
| 12 |
| 1 |
| 12 |
∴tanαcotβ=5,正确.
故答案为:③④.
点评:本题是综合题,考查函数与导数的关系最值的求法,两角和与差的三角函数,函数的定义域的求法,基本不等式的应用,考查计算能力.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
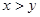 ,则
,则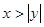 ”的逆命题
”的逆命题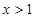 ,则
,则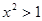 ”的否命题
”的否命题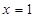 ,则
,则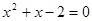 ”的否命题
”的否命题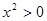 ,则
,则