题目内容
(2013•盐城二模)若等比数列{an}满足am-3=4且amam-4=
(m∈N*且m>4),则a1a5的值为
| a | 2 4 |
16
16
.分析:依题意,可知m+(m-4)=8,可求得m=6,从而可知a3=4,再利用等比数列的性质即可求得a1a5的值.
解答:解:∵数列{an}为等比数列,amam-4=a42(m∈N*且m>4),
∴m-4,4,m成等差数列,
∴m+(m-4)=8,
解得:m=6.
∴am-3=a3=4.
又a1,a3,a5成等比数列,
∴a1a5=a32=16.
故答案为:16.
∴m-4,4,m成等差数列,
∴m+(m-4)=8,
解得:m=6.
∴am-3=a3=4.
又a1,a3,a5成等比数列,
∴a1a5=a32=16.
故答案为:16.
点评:本题考查等比数列的性质,考查观察、分析与运算能力,属于中档题.

练习册系列答案
相关题目
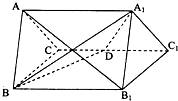 (2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.
(2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.