题目内容
 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,PB与平面ABC成60°的角,底面ABCD是直角梯形,∠ABC=∠BAD=90°,AB=BC=
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,PB与平面ABC成60°的角,底面ABCD是直角梯形,∠ABC=∠BAD=90°,AB=BC= AD.
AD.
(1)求证:平面PCD⊥平面PAC;
(2)设E是棱PD上一点,且PE= PD,求异面直线AE与PB所成的角.
PD,求异面直线AE与PB所成的角.
解:如图,建立空间直角坐标系A-xyz.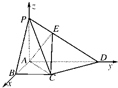
∵PA⊥平面ABCD,PB与平面ABC成60°,
∴∠PBA=60°,∴PA=ABtan60°= .
.
取AB=1,则A(0,0,0),B(1,0,0),C(1,1,0),P(0,0, ),D(0,2,0).
),D(0,2,0).
(1)∵ =(1,1,0),
=(1,1,0), =(0,0,
=(0,0, ),
), =(-1,1,0),
=(-1,1,0),
∴ •
• =-1+1+0=0,
=-1+1+0=0, •
• =0.
=0.
∴AC⊥CD,AP⊥CD,
∵AC∩AP=A,
∴CD⊥平面PAC.
又CD?平面PCD,
∴平面PCD⊥平面PAC.
(2)∵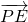 =
=
 ,
,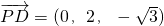 ,
,
∴ =(0,0,
=(0,0, )+
)+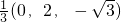 =
=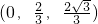 ,
,
∴E(0, ,
, ),∴
),∴ =(0,
=(0, ,
, ).
).
又 =(1,0,-
=(1,0,- ),∴
),∴ •
• =-2.
=-2.
∴cos< •
• >=
>=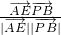 =
=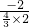 =-
=- .
.
∴异面直线AE与PB所成的角为arccos .
.
分析:先建立空间直角坐标系,写出有关的点及向量的坐标.(1)利用 ?
? ,来证明线线垂直,从而证明线面、面面垂直;(2)先求出两条异面直线的方向向量,进而利用向量的夹角即可求出异面直线所成的夹角.
,来证明线线垂直,从而证明线面、面面垂直;(2)先求出两条异面直线的方向向量,进而利用向量的夹角即可求出异面直线所成的夹角.
点评:熟练掌握通过建立空间直角坐标系利用平面的法向量和直线的方向向量等知识证明线线、线面、面面垂直和求出异面直线所成的夹角的方法是解题的关键.

∵PA⊥平面ABCD,PB与平面ABC成60°,
∴∠PBA=60°,∴PA=ABtan60°=
 .
.取AB=1,则A(0,0,0),B(1,0,0),C(1,1,0),P(0,0,
 ),D(0,2,0).
),D(0,2,0).(1)∵
 =(1,1,0),
=(1,1,0), =(0,0,
=(0,0, ),
), =(-1,1,0),
=(-1,1,0),∴
 •
• =-1+1+0=0,
=-1+1+0=0, •
• =0.
=0.∴AC⊥CD,AP⊥CD,
∵AC∩AP=A,
∴CD⊥平面PAC.
又CD?平面PCD,
∴平面PCD⊥平面PAC.
(2)∵
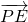 =
=
 ,
,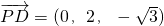 ,
,∴
 =(0,0,
=(0,0, )+
)+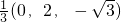 =
=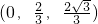 ,
,∴E(0,
 ,
, ),∴
),∴ =(0,
=(0, ,
, ).
).又
 =(1,0,-
=(1,0,- ),∴
),∴ •
• =-2.
=-2.∴cos<
 •
• >=
>=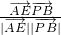 =
=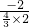 =-
=- .
.∴异面直线AE与PB所成的角为arccos
 .
.分析:先建立空间直角坐标系,写出有关的点及向量的坐标.(1)利用
 ?
? ,来证明线线垂直,从而证明线面、面面垂直;(2)先求出两条异面直线的方向向量,进而利用向量的夹角即可求出异面直线所成的夹角.
,来证明线线垂直,从而证明线面、面面垂直;(2)先求出两条异面直线的方向向量,进而利用向量的夹角即可求出异面直线所成的夹角.点评:熟练掌握通过建立空间直角坐标系利用平面的法向量和直线的方向向量等知识证明线线、线面、面面垂直和求出异面直线所成的夹角的方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a, 如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点
如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点 (2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.
(2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.