题目内容
若△ABC的内角A满足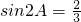
，则sinA+cosA=
- A.
- B.
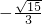
- C.
- D.
A
分析：根据（sinA+cosA）2=1+sin2A，即得答案．
解答：由sin2A=2sinAcosA＞0，可知A这锐角，
所以sinA+cosA＞0，
又
，
故选A．
点评：考查同角三角函数间的基本关系．
分析：根据（sinA+cosA）2=1+sin2A，即得答案．
解答：由sin2A=2sinAcosA＞0，可知A这锐角，
所以sinA+cosA＞0，
又
，故选A．
点评：考查同角三角函数间的基本关系．
练习册系列答案
相关题目
） B．[0，1] C．（
） D．（
）
） B．[0，1] C．（
） D．（
）