题目内容
已知2f(x)+f(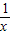 )=-
)=-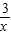 (x≠0),则下列说法正确的是( )
(x≠0),则下列说法正确的是( )A.f(x)为奇函数且在(-∞,0)上为增函数
B.f(x)为奇函数且在(-∞,0)上为减函数
C.f(x)为偶函数且在(-∞,0)上为增函数
D.f(x)为偶函数且在(-∞,0)上为减函数
【答案】分析:使用方程组法,可以求出函数f(x)的解析式,进而根据函数奇偶性的定义和函数单调性的性质,判断出函数的奇偶性和单调性可得答案.
解答:解:∵2f(x)+f(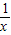 )=-
)=-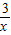 …①
…①
∴2f(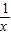 )+f(x)=-3x…②
)+f(x)=-3x…②
①×2-②得
3f(x)=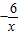 +3x
+3x
∴f(x)=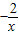 +x
+x
易得在x≠0时,f(-x)=-f(x)恒成立,故函数为奇函数
又∵在(-∞,0)上y=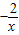 为增函数,y=x也为增函数
为增函数,y=x也为增函数
∴f(x)=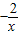 +x在(-∞,0)上为增函数
+x在(-∞,0)上为增函数
故选A
点评:本题考查的知识点是函数奇偶性的判断,函数解析的求法,函数单调性的性质,其中利用方程组法求出函数的解析式是解答的关键.
解答:解:∵2f(x)+f(
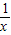 )=-
)=-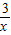 …①
…①∴2f(
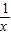 )+f(x)=-3x…②
)+f(x)=-3x…②①×2-②得
3f(x)=
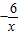 +3x
+3x∴f(x)=
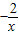 +x
+x易得在x≠0时,f(-x)=-f(x)恒成立,故函数为奇函数
又∵在(-∞,0)上y=
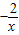 为增函数,y=x也为增函数
为增函数,y=x也为增函数∴f(x)=
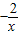 +x在(-∞,0)上为增函数
+x在(-∞,0)上为增函数故选A
点评:本题考查的知识点是函数奇偶性的判断,函数解析的求法,函数单调性的性质,其中利用方程组法求出函数的解析式是解答的关键.

练习册系列答案
相关题目
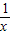 )=
)=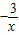 (x≠0),则下列说法正确的为( )
(x≠0),则下列说法正确的为( )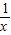 )=
)=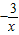 (x≠0),则下列说法正确的为( )
(x≠0),则下列说法正确的为( )