Question

(本小题满分12分)

已知函数f(x)=4x3-3x2sin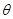+的极小值大于零,其中x∈R, 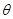∈[0,].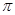

(1).求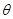的取值范围.

(2).若在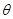的取值范围内的任意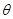,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.

(3).设x0＞,f(x0) ＞,若f[f(x0)]=x0,求证f(x0)=x0

 

Answer 1

【答案】

 

(1)

(2)

(3)略

【解析】解：（1）

         令   则

              

x		0
	+	0	_	0	+
		极大值		极小值

 

        

----------------------------------（4分）

   （2）由（1）知内为增函数

        或

        -----------------------------------（8分）

（3）证明：假设则

         ,

       

       

        或

        矛盾

        假设不成立 ---------------------------（12分）