题目内容
在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外切圆面积为S2,则  =
= ,推广到空间可以得到类似结论,已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则
,推广到空间可以得到类似结论,已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则 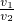 =
=
- A.

- B.

- C.

- D.

C
分析:平面图形类比空间图形,二维类比三维得到,类比平面几何的结论,确定正四面体的外接球和内切球的半径之比,即可求得结论.
解答: 解:从平面图形类比空间图形,从二维类比三维,
解:从平面图形类比空间图形,从二维类比三维,
如图,设正四面体的棱长为a,则AE=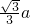 ,DE=
,DE=
设OA=R,OE=r,则
∴R= ,r=
,r=
∴正四面体的外接球和内切球的半径之比是 3:1
故正四面体P-ABC的内切球体积为V1,外接球体积为V2之比等于
故选C
点评:本题考查类比推理,考查学生的计算能力,正确计算是关键.
分析:平面图形类比空间图形,二维类比三维得到,类比平面几何的结论,确定正四面体的外接球和内切球的半径之比,即可求得结论.
解答:
 解:从平面图形类比空间图形,从二维类比三维,
解:从平面图形类比空间图形,从二维类比三维,如图,设正四面体的棱长为a,则AE=
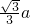 ,DE=
,DE=
设OA=R,OE=r,则

∴R=
 ,r=
,r=
∴正四面体的外接球和内切球的半径之比是 3:1
故正四面体P-ABC的内切球体积为V1,外接球体积为V2之比等于

故选C
点评:本题考查类比推理,考查学生的计算能力,正确计算是关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 ,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则
,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则 ( )
( ) B.
B. C.
C. D.
D.
 ,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则
,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则 ( )
( ) B.
B. C.
C. D.
D.