题目内容
17.某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中任取3所学校做进一步数据分析,①求取出的3所学校中没有小学的概率;②设取出的小学个数为随机变量X,求X的分布列和数学期望.
分析 (1)利用分层抽样的意义,先确定抽样比,在确定每层中抽取的学校数目;
(2)①利用古典概型概率的计算方法,可得结论;
②X的取值为0,1,2,3,求出相应的概率,即可求X的分布列和数学期望.
解答 解:(1)从小学、中学、大学中抽取的抽样比为$\frac{6}{21+14+7}$=$\frac{1}{7}$
∴从小学、中学、大学中分别抽取的学校数目为3,2,1.
(2)①从6所学校中任取的3所学校没有小学(记为事件B)的概率为P(B)=$\frac{1}{{C}_{6}^{3}}$=$\frac{1}{20}$.
②X的取值为0,1,2,3,则
P(X=0)=$\frac{1}{20}$,P(X=1)=$\frac{{C}_{3}^{1}{C}_{3}^{2}}{{C}_{6}^{3}}$=$\frac{9}{20}$,P(X=2)=$\frac{{C}_{3}^{2}{C}_{3}^{1}}{{C}_{6}^{3}}$=$\frac{9}{20}$,P(X=3)=$\frac{1}{20}$
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{20}$ | $\frac{9}{20}$ | $\frac{9}{20}$ | $\frac{1}{20}$ |
点评 本题主要考查了统计中分层抽样的意义,古典概型概率的计算方法,列考查求X的分布列和数学期望,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.数列$\left\{{tan\frac{n}{9}π•tan\frac{n+1}{9}π}\right\}$的前n项和记为Sn,则S2015=( )
| A. | -2016 | B. | -2015 | C. | -2014 | D. | -1007 |
12.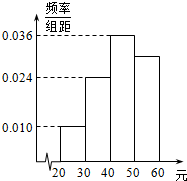 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元.
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元.
 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元.
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元.| A. | 45 | B. | 46 | C. | $\frac{390}{9}$ | D. | $\frac{400}{9}$ |
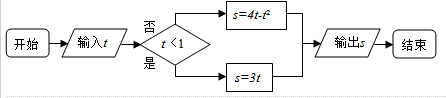
9.某程序框图如图所示,当输出y值为-8时,则输出x的值为( )


| A. | 64 | B. | 32 | C. | 16 | D. | 8 |
6.已知长方体ABCD-A1B1C1D1,从一个顶点出发的三条棱长分别为1、1、2,顶点A、B、C、D在半球的底面内,顶点A1、B1、C1、D1在半球球面上,则此半球的体积是( )
| A. | $\frac{\sqrt{6}}{2}$π | B. | $\frac{9\sqrt{2}}{2}$π | C. | $\frac{9}{4}$π | D. | $\frac{9\sqrt{2}}{2}$π或$\frac{9π}{4}$ |