题目内容
设等差数列{an}的前n项和为Sn,且a1=2,a3=6.
(1)求数列{an}的通项公式;
(2)设数列{
}的前n项和为Tn,求T2013的值.
(1)求数列{an}的通项公式;
(2)设数列{
| 1 |
| Sn |
(本小题满分12分)
(1)设等差数列{an}的公差为d,
∵a1=2,a3=6,
∴
,解得a1=2,d=2,
∴数列{an}的通项公式an=2+(n-1)•2=2n.
(2)∵a1=2,d=2,
∴Sn=
=n(n+1),
∴
=
=
-
∴T2013=T1+T2+T3+…+T2013
=(1-
)+(
-
)+(
-
)+…+(
-
)
=1-
=
.
(1)设等差数列{an}的公差为d,
∵a1=2,a3=6,
∴
|
∴数列{an}的通项公式an=2+(n-1)•2=2n.
(2)∵a1=2,d=2,
∴Sn=
| n(2+2n) |
| 2 |
∴
| 1 |
| Sn |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴T2013=T1+T2+T3+…+T2013
=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2013 |
| 1 |
| 2014 |
=1-
| 1 |
| 2014 |
| 2013 |
| 2014 |

练习册系列答案
相关题目
 +
+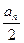 (n∈N+),则其{an}的前10项和为
(n∈N+),则其{an}的前10项和为