题目内容
设点
动圆P经过点F且和直线
相切，记动圆的圆心P的轨迹为曲线W。
（1）求曲线W的方程；
（2）过点F作互相垂直的直线
，分别交曲线W于A，B和C，D。求四边形ABCD面积的最小值。
（3）分别在A、B两点作曲线W的切线，这两条切线的交点记为Q。
求证：QA⊥QB，且点Q在某一定直线上。
【答案】
（2）依题意，直线l1,l2的斜率存在且不为0，
解：（1）过点P作PN垂直于直线
于点N
依题意得
所以动点P的轨迹是以
为焦点，直线为准线的抛物线。…………（1分）
即曲线W的方程是
………………（2分）
|
设直线l1的方程为
由l1⊥l2得l2的方程为
将
…………………………（3分）
设
∴
同理可得
……………………（5分）
∴四边形ABCD的面积
当且仅当
故四边形ACBD面积的最小值是72。……………………（7分）
（3）由（1）知W的方程可化为
∴
∵QA的斜率
∴
∴QA⊥QB…………………………（9分）
QA的方程为
QB的方程为
解方程组
即Q（2k，
）………………（11分）
当k取任何非零实数时，点Q总在定直线y=上………………（12分）
练习册系列答案
阅读快车系列答案
相关题目
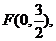动圆P经过点F且和直线
相切，记动圆的圆心P的轨迹为曲线W。
，分别交曲线W于A，B和C，D。求四边形ABCD面积的最小值。
动圆P经过点F且和直线
相切，记动圆的圆心P的轨迹为曲线W。
，分别交曲线W于A，B和C，D。求四边形ABCD面积的最小值。