Question

请针对某工厂产品与单位成本的资料进行分析：

月份	1	2	3	4	5	6
产量x(千件)	2	3	4	3	4	5
单位成本y(元/件)	73	72	71	73	69	68

Answer 1

思路分析：本题考查线性回归直线方程的求法及利用线性回归直线方程处理问题的方法.

解：设回归直线方程为=bx+a.列表如下：

I	1	2	3	4	5	6
xi	2	3	4	3	4	5
yi	73	72	71	73	69	68
xiyi	146	216	284	219	276	340

b=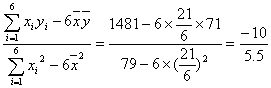=-1.818 2,

a=-b=71-(-1.818 2)×≈77.36.

所以，回归直线方程为=77.36-1.818 2x.

由于线性回归系数b为-1.818 2，

由回归系数b的意义可知产量每增加1 000件，单位成本下降1.818 2元.