题目内容
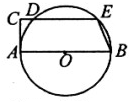（2013•和平区一模）如图，已知AB为圆O的直径，AC与圆O相切于点A，CE∥AB交圆O于D、E两点，若AB=2，CD=| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
分析：利用矩形和圆的性质可得2CD+DE=AB=2，即可得到CE．再利用切割线定理和勾股定理即可得出AD，再利用同圆的等弧所对的弦相等即可得出．
解答：解：设CD=
，则2×
+DE=2，解得DE=
，∴CE=CD+DE=
．
∵AC与圆O相切于点A，∴AC⊥AB，AC2=CD•CE=
×
=
．
∴AD2=AC2+CD2=
+
=
，解得AD=
．
∵CE∥AB，∴
=
，∴BE=AD=
．
故答案为
．
| 2 |
| 9 |
| 2 |
| 9 |
| 14 |
| 9 |
| 16 |
| 9 |
∵AC与圆O相切于点A，∴AC⊥AB，AC2=CD•CE=
| 2 |
| 9 |
| 16 |
| 9 |
| 32 |
| 81 |
∴AD2=AC2+CD2=
| 32 |
| 81 |
| 4 |
| 81 |
| 36 |
| 81 |
| 2 |
| 3 |
∵CE∥AB，∴
 |
| AD |
|
| BE |
| 2 |
| 3 |
故答案为
| 2 |
| 3 |
点评：熟练掌握矩形和圆的性质、切割线定理和勾股定理、同圆的等弧所对的弦相等是解题的关键．
练习册系列答案
相关题目
（2013•和平区一模）在如图所示的计算1+3+5+…+2013的值的程序框图中，判断框内应填入（ ）